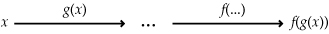
Theorie

Een samengestelde functie is een functie die uit twee of meer in serie geschakelde functies bestaat. Voor de afgeleide van een samengestelde functie geldt

Differentieerregel 4 (kettingregel):
Als S(x) = f(g(x)) dan is S'(x) = f'(g(x)) · g'(x).

» Bewijs

Met behulp van deze regel bewijs je ook de machtsregel voor wortelfuncties:

Als $f(x)=\sqrt[n]{x}=x^{\frac{1}{n}}$  dan is $f\text{'}(x)=\frac{1}{n}{x}^{\frac{1}{n}-1}$ voor gehele positieve n en x ≠ 0.

» Bewijs

In het algemeen geldt:

Differentieerregel 5 (algemene machtsregel):
Als f(x) = x^r dan is f'(x) = rx^r – 1 voor elke reële waarde van r.

Voor het bewijs van deze differentieerregel moet je eerst leren exponentiële functies en logaritmische functies te differentiëren. Dat komt later.