Uitleg
Soms bestaat een functievoorschrift uit in serie geschakelde functies.
Neem bijvoorbeeld S(x) = (2x + 10)3.
Een functiewaarde bereken je nu in twee stappen:
- eerst bereken je g(x) = 2x + 10;
- vervolgens f(g(x)) = (g(x))3.
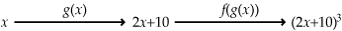
De functie S(x) = (2x + 10)3 = (g(x))3 = f(g(x)) heet een samengestelde functie of kettingfunctie.
Deze kettingfunctie kun je differentiëren door met transformaties te werken:
S'(x) = 3(2x + 10)2 · 2 = 6(2x + 10)2.
Dat gaat echter alleen maar omdat g(x) = 2x + 10 lineair is.
En als de exponent geen geheel getal is kun je ook de haakjes niet uitwerken...
Het differentiëren van een kettingfunctie vereist in het algemeen een speciale differentieerregel: de kettingregel. Om die af te leiden gebruik je de lineaire benadering. Je vindt de afleiding van de kettingregel bij de theorie.
