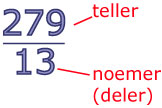
Theorie

Alle getallen die je als breuk kunt schrijven noem je rationale getallen ("ratio" betekent "verhouding"), ze vormen de verzameling $\mathbb{Q}$ = { $\frac{p}{q}$ | p $\in$ $\mathbb{Z}$ en q $\in$ $\mathbb{Z}$ en q ≠ 0}.
Omdat je elk geheel getal als breuk kunt schrijven zijn de gehele getallen een deelverzameling van de rationale getallen: $\mathbb{Z}$ $\subset$ $\mathbb{Q}$.

Kenmerkend voor de rationale getallen is dat de som, het verschil, het product en het quotiënt van twee rationale getallen altijd weer een rationaal getal is. (Voor de gehele getallen geldt dit niet, immers bij delen krijg je niet altijd weer een geheel getal.)

Met behulp van een staartdeling kun je van een rationaal getal een decimaal getal maken. Er zijn dan twee mogelijkheden:

• De staartdeling komt op 0 uit, dus het getal heeft een eindig aantal decimalen.
  Bijvoorbeeld: $\frac{1}{5}$ = 0,2 en $\frac{3}{8}$ = 0,375.
• De staartdeling komt nooit op 0 uit, dus het getal heeft een oneindig aantal decimalen. Er treedt dan altijd herhaling van decimalen op.
  Bijvoorbeeld: $\frac{1}{9}$ = 0,11111111... = 0,1 en $\frac{6}{13}$ = 0,461538.