Theorie

Een lijn en een cirkel hebben geen, één of twee punten gemeenschappelijk. Hebben een lijn en een cirkel twee punten gemeen, dan snijden ze elkaar.
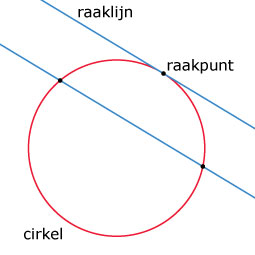
Hebben een lijn en een cirkel maar één punt gemeen (beide snijpunten vallen dan samen), dan zeg je dat ze elkaar raken. De lijn is een raaklijn aan de cirkel.

Om snijpunten te berekenen van een lijn en een cirkel gebruik je de vergelijking van de lijn en die van de cirkel: je combineert het bijbehorende stelsel vergelijkingen tot één kwadratische vergelijking met één onbekende.
Je kunt deze kwadratische vergelijking schrijven als ax² + bx + c = 0.
De oplossingen zijn dan: x = $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$.
Deze formule heet de abc-formule.

Als de lijn en de cirkel elkaar raken dan heeft deze kwadratische vergelijking met één onbekende maar één oplossing.
De discriminant D = b² – 4ac van deze vergelijking is dan 0. Daarvan kun je gebruik maken bij het opstellen van vergelijkingen van raaklijnen, bekijk de Voorbeelden maar...