Voorbeeld 2

De hellingsfunctie zegt veel over het verloop van een grafiek. Het gaat er dan vooral om waar de hellingen positief negatief of 0 zijn. Daarvoor heb je geen hellingsgrafiek nodig, een tekenschema van de afgeleide is genoeg.
Je ziet hier een tekenschema van de hellingsfunctie van een onbekende functie f.

Schets een mogelijke grafiek van f.

Antwoord

Als de hellingsfunctie positief is de grafiek van f stijgend, als de hellingsfunctie negatief is die grafiek dalend. Welke waarden f(x) precies aanneemt is niet bekend.
Kies een startpunt, bijvoorbeeld (0,0). De helling is daar negatief, dus de grafiek dalend. Hoe steil, is onbekend. Verder heeft de grafiek een maximum als x = –1 omdat daar de helling overgaat van positief in negatief. Een minimum treedt op als x = 2 omdat dan de helling van negatief in positief verandert.
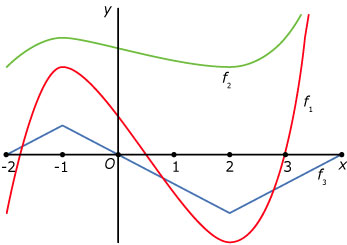
Hier zie je drie mogelijke grafieken. Maar er zijn nog veel meer mogelijkheden. De grafieken hoeven niet door (0,0) te gaan.