Uitleg

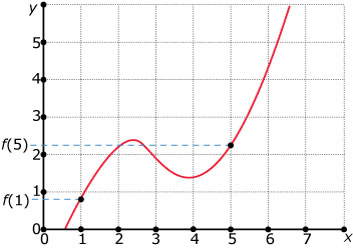
In het algemeen heb je te maken met y als functie van x: y = f(x).

Stel dat x toeneemt van bijvoorbeeld x = 1 tot x = 5.
Dan is de toename Δx = 5 – 1 = 4.
Tegelijk verandert y van f(1) naar f(5).
Dus een toename (of afname) van f(5) – f(1).

Gemiddeld (dus per eenheid van x) verandert y op het interval [1, 5] met:

$\frac{\Delta y}{\Delta x}=\frac{f(5)-f(1)}{5-1}$

En dit is een deling van twee verschillen, een zogenaamd differentiequotiënt ("differentie" is "verschil" en een quotiënt is de uitkomst van een deling).
Op deze manier bereken je bij elke functie de gemiddelde verandering van y op een gegeven interval.