Uitleg

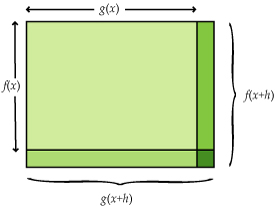
Als lengte en breedte van een rechthoek functies van x zijn, is de oppervlakte A een productfunctie in x: A(x) = f(x) · g(x).
Je kunt de oppervlakte van deze rechthoek variëren door x te laten toenemen tot x + h. De nieuwe oppervlakte is:
A(x + h) = f(x + h) · g(x + h) en:

$A\text{'}(x)=\underset{h\to 0}{\lim }\frac{A(x+h)-A(x)}{h}=\underset{h\to 0}{\lim }\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Met behulp van lineaire benadering van f(x + h) en g(x + h) wordt dit:
A'(x) = $\underset{h\to 0}{\lim }\frac{(f(x)+h\cdot f\text{'}(x))(g(x)+h\cdot g\text{'}(x))-f(x)\cdot g(x)}{h}$ =
        = $\underset{h\to 0}{\lim }\frac{h\cdot f\text{'}(x)\cdot g(x)+h\cdot f(x)\cdot g\text{'}(x)+h^2\cdot f\text{'}(x)\cdot g\text{'}(x)}{h}$

In de figuur is A'(x) het totaal van de drie donkerder rechthoekjes (als h naar 0).
Boven de breukstreep kun je in de drie termen de verschillende rechthoekjes herkennen.

En dus is $A\text{'}(x)=\underset{h\to 0}{\lim }\left(f\text{'}(x)\cdot g(x)+f(x)\cdot g\text{'}(x)+h\cdot f\text{'}(x)\cdot g\text{'}(x)\right)=f\text{'}(x)\cdot g(x)+f(x)\cdot g\text{'}(x)$.

Je hebt nu een manier gevonden om de afgeleide van een productfunctie te bepalen. Tenminste als f en g stijgende functies zijn met positieve functiewaarden.