Uitleg

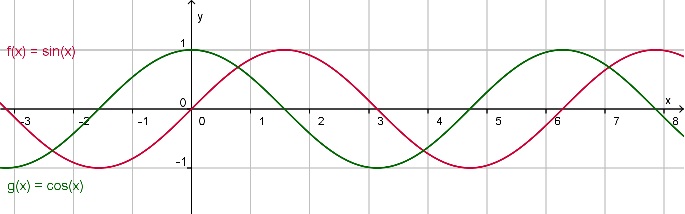
Je kent de functies f(x) = sin(x) en g(x) = cos(x) met x in radialen al. Omdat in de functies die trillingen beschrijven sinus en cosinus voorkomen, zijn het voorbeelden van goniometrische functies. De belangrijkste eigenschap is wel hun periodiciteit. De periode van deze functies is 2π. Hun amplitude is 1.

Bekijk je nu de functie u₂(t) = 0,8 sin(880 · 2π · t), dan worden alle waarden van sin(880 · 2π · t) met 0,8 vermenigvuldigd en dus is de amplitude 0,8.
Verder worden alle waarden van t met 880 · 2π vermenigvuldigd. Loopt t van 0 naar 1 dan worden er 880 periodes doorlopen. Elke herhaling duurt daarom 1/880 seconde.
Maar verder heeft de grafiek van u₂(t) = 0,8 sin(880 · 2π · t) dezelfde vorm als die van f(x) = sin(x). Maar wat als je sin(x) en/of cos(x) gaat gebruiken om ingewikkelder functievoorschriften te maken? Bekijk eerst maar eens een paar grafieken.