Uitleg
Als je een vergelijking zoals x2 + y2 + 6x = 0 bij een kromme lijn ziet staan, hoe weet je dan zeker of de kromme een cirkel is?
Vergelijkingen van cirkels hebben de vorm (x – a)2 + (y – b)2 = r2 waarin het middelpunt M(a,b) en de straal r is.
De vraag is daarom: kun je de gegeven vergelijking in die vorm schrijven?
Met y2 heb je geen moeite, dat is (y – 0)2.
Maar x2 + 6x ligt anders.
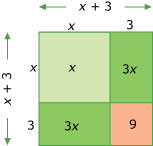
Bekijk de figuur en ga na, dat
(x + 3)2 = x2 + 6x + 9 en dus
x2 + 6x = (x + 3)2 – 9.
Dit noem je een kwadraat afsplitsen.
Je hebt van de vorm x2 + 6x een kwadraat afgesplitst. Merk op dat je de term 6x moet lezen als 2 · 3x.
De gegeven vergelijking kun je nu schrijven als (x + 3)2 – 9 + (y – 0)2 = 0 en dus als
(x + 3)2 + (y – 0)2 = 9.
Het is daarom de vergelijking van een cirkel met middelpunt M(–3,0) en straal 3.