Voorbeeld

Gegeven de twee harmonische trillingen u₁ en u₂ door:
u₁(t) = 2 sin(t) + 1 en u₂(t) = sin(t – 2).
Beide trillingen hebben alleen dezelfde periode. Toon aan dat u = u₁ + u₂ ook een harmonische trilling is.

Antwoord

Omdat de amplitudes verschillen kun je de formules van Simpson niet toepassen. Wel kun je sin(t – 2) uitwerken:
sin(t – 2) = sin(t) cos(2) – cos(t) sin(2).

Hiermee wordt: u(t) ≈ 1,58 sin(t) – 0,91 cos(t) + 1.
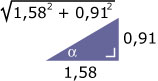
Nu is er een hoek α met: cos(α) = $\frac{\mathrm{1,58}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$  en  sin(α) = $\frac{\mathrm{0,91}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$
En dus is:
u(t) ≈ $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · (sin(t) · $\frac{\mathrm{1,58}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$ – cos(t) · $\frac{\mathrm{0,91}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$) + 1 = 
       = $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · (sin(t) cos(α) – cos(t) sin(α)) + 1 =
       = $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · sin(t – α) + 1
De hoek α bereken je uit tan(α) = $\frac{\mathrm{0,91}}{\mathrm{1,58}}$.

u is een harmonische trilling met u(t) ≈ $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · sin(t – 0,52) + 1.