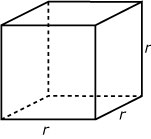
Uitleg

De inhoud van een kubus met ribben van lengte r is: I = r · r · r = r³.
Dit is een typisch voorbeeld van een machtsfunctie: de variabele r moet tot de derde macht worden verheven om een functiewaarde te vinden. Als r = 5, dan is I = 5³ = 125.

Al in de Oudheid vroegen de Grieken zich af hoe groot nu de ribbe is van een kubus die een inhoud heeft die precies het dubbele is van de gegeven inhoud. In ons geval: "Hoe groot is de ribbe van een kubus met een inhoud van 250?"
De oplossing van deze vraag is tegelijk eenvoudig als heel erg moeilijk. Want net als bij terugrekenen van uit een kwadraat door worteltrekken kun je terugrekenen vanuit een derde macht. Dat heet dan een derde machts wortel.
De gevraagde oplossing is dan r = $\sqrt[3]{250}$.

Het moeilijke hieraan is dat deze oplossing geen getal is dat je in alle decimalen kunt berekenen; je kunt het slechts benaderen (door inklemmen). Je rekenmachine kan dit snel voor je doen: r = $\sqrt[3]{250}$ ≈ 6,299605 als het in zes decimalen nauwkeurig moet.

Een andere schrijfwijze voor de oplossing van r³ = 250 is: r = ${250}^{\frac{1}{3}}$.
Immers: ${\left({250}^{\frac{1}{3}}\right)}^3$  = 250. Je ziet: $\sqrt[3]{250}$ = ${250}^{\frac{1}{3}}$.