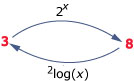
Theorie

De oplossing van de logaritmische vergelijking ^glog(x) = a vind je door aan beide zijden een exponentiële functie met grondtal g toe te passen.
Uit ^glog(x) = a volgt dan x = g^a.
Hierbij moet g > 0 en g ≠ 1 en a > 0.

De logaritmische ongelijkheid ^glog(x) < a los je op m.b.v. grafieken:

• Eerst los je de bijbehorende vergelijking ^glog(x) = a op.
• Vervolgens bekijk je de grafieken van y₁ = ^glog(x) en y₂ = a. Daarbij moet je vooral letten op het domein (en de verticale asymptoot) van de logaritme.
• De oplossing lees je uit de grafiek af.