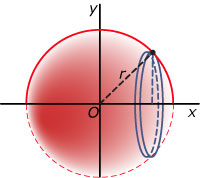
Voorbeeld

Een bol met straal r en middelpunt O ontstaat door de grafiek van f(x) = $\sqrt{r^2-x^2}$ op het interval [–r,r] om de x-as te wentelen.
Stel een formule op voor de inhoud en één voor de oppervlakte van die bol.

Antwoord

Voor de inhoud van de bol geldt:
I(bol) = ${{\displaystyle \underset{-r}{\overset{r}{\int }}\text{π}\left(\sqrt{r^2-x^2}\right)}}^2\text{d}x$ = ${\displaystyle \underset{-r}{\overset{r}{\int }}\text{π(}{r}^2-x^2)}\text{d}x$ = $\frac{4}{3}$πr³

De oppervlakte A(r) van de bol kun je uit I(r) afleiden.
Bedenk, dat bij toename van r met een heel klein beetje Δr = h de inhoud toeneemt met I(r + h) – I(r). De oppervlakte van deze laag met een dikte h is ongeveer de gevraagde oppervlakte en gelijk aan $\frac{I(r+h)-I(r)}{h}$.
Deze benadering wordt beter naarmate h naar 0 nadert.
En daarom is A(r) = $\underset{h\to 0}{\lim }\frac{I(r+h)-I(r)}{h}$ = I'(r).
Dit betekent dat de oppervlakte van de bol is: A(r) = 4πr².