Uitleg

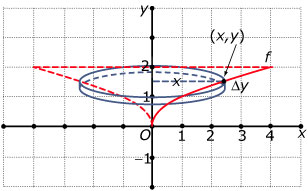
Je ziet hier hoe het vlakdeel ingesloten door de grafiek van f(x) = $\sqrt{x}$  en de y-as op het interval [0,4] om de y-as wordt gewenteld.
Dit vlakdeel wordt ook begrensd door de lijn y = 2. Het omwentelingslichaam dat zo ontstaat kun je benaderen door smalle cilinders door op de y-as het interval [0,2] in deelintervallen met een breedte van Δy te verdelen. De inhoud van zo'n cilinder is πx² · Δy.
Als het aantal deelintervallen oneindig groot wordt, dat gaat Δy naar 0 en de inhoud van het omwentelingslichaam wordt een integraal van de vorm:
I = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}{x}^2\text{d}y}$

Deze integraal kun je berekenen door het functievoorschrift y = $\sqrt{x}$ te herschrijven naar x = y².

De inhoud van het omwentelingslichaam wordt dan:
I = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}{(y^2)}^2\text{d}y}$ = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}{y}^4\text{d}y}$ = ${\left[\frac{1}{5}\text{π}{y}^5\right]}_0^2$ = 6,4π