Voorbeeld

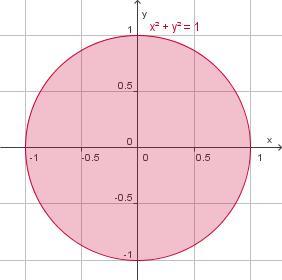
Bereken m.b.v. integreren de oppervlakte en de omtrek van de cirkel c met middelpunt O en straal 1 in twee decimalen nauwkeurig.

Antwoord

Omdat voor elk punt van de cirkel geldt x² + y² = 1, kun je hem beschrijven met twee functies: y₁ = $\sqrt{1-x^2}$ en y₂ = –$\sqrt{1-x^2}$.
Voor de berekening van oppervlakte en omtrek kijk je alleen naar de bovenste helft, dus y₁.

opp(c) = 2 · ${\displaystyle \underset{-1}{\overset{1}{\int }}\sqrt{1-x^2}}\text{d}x$ ≈ 3,14.

L(c) = 2 · ${\displaystyle \underset{-1}{\overset{1}{\int }}\sqrt{1+{\left(\frac{-x}{\sqrt{1-x^2}}\right)}^2}}\text{d}x={\displaystyle \underset{-1}{\overset{1}{\int }}\sqrt{1+\frac{x^2}{1-x^2}}\text{d}x}$ ≈ 6,28.

Denk er om dat je niet hebt bewezen dat de oppervlakte π en de omtrek 2π is. Je hebt ze alleen benaderd met je GR. Je kunt met integreren ook gemakkelijk de oppervlakte van een deel van de cirkel berekenen...