Voorbeeld

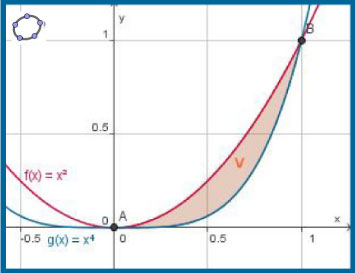
Bereken de omtrek van het vlakdeel V ingesloten door de grafieken van f(x) = x² en g(x) = x⁴ op het interval [0,1]. Geef een benadering in drie decimalen nauwkeurig.

Antwoord

De omtrek van V is de som van de lengte L_f van de grafiek van f op interval [0,1] en de lengte L_g van de grafiek van g op datzelfde interval.
Nu is f'(x) = 2x en g(x) = 4x³.
En dus is de omtrek van V:

L_f + L_g = ${\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+{(2x)}^2}}\text{d}x+{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+{(4x^3)}^2}}\text{d}x$

Beide integralen zijn alleen met de grafische rekenmachine te bepalen.
Ga na dat de omtrek van V ongeveer 1,479 + 1,600 = 3,079.