Voorbeeld

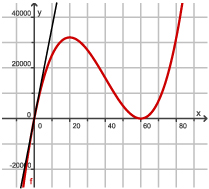
Hier zie je de grafiek van f(x) = x(60 – x)² uit voorbeeld 2 nog eens.
Nu is de raaklijn aan de grafiek van f in (0,0) getekend.
Welke hoek maakt deze raaklijn met de x-as?
Zijn er andere punten op de grafiek van f waarin de raaklijn dezelfde hoek met de x-as maakt?

Antwoord

In voorbeeld 2 is de afgeleide van f bepaald: f'(x) = 3600 – 240x + 3x².
Dus f'(0) = 3600.

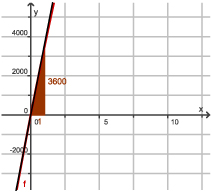
In de figuur zie je na inzoomen dat tan(α) = $\frac{3600}{1}$ = 3600 als α de gevraagde hoek is. Hieruit vind je: α ≈89,98°.

Vervolgens zoek je andere punten van de grafiek waarin de raaklijn dezelfde hoek met de x-as maakt. Omdat die hoek bepaald wordt door het hellingsgetal, weet je dat in die punten de afgeleide gelijk is aan 3600 of aan –3600.
Dus moet je oplossen: f'(x) = 3600  V  f'(x) = –3600.
Ga na dat dit oplevert: x = 0  V  x = 80, want de vergelijking f'(x) = –3600 heeft geen oplossingen.
Het enige andere punt waarin de raaklijn dezelfde hoek met de x-as maakt is (80,24000).