Voorbeeld

Gegeven is de functie f met f(x) = x(60 – x)².
Bereken algebraïsch de extremen van f en het buigpunt van de grafiek van f.

Antwoord

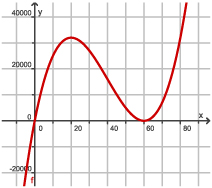
Je ziet een nette grafiek van f. Er lijken twee extremen en één buigpunt te zijn. Zeker weet je dat pas na differentiëren.
Om de afgeleide te kunnen bepalen moeten eerst de haakjes worden uitgewerkt:

f(x) = x(60 – x)² = 3600x – 120x² + x³.

De afgeleide is dan: f'(x) = 3600 – 240x + 3x².
De tweede afgeleide is: f"(x) = –240 + 6x.

Voor de extremen moet je oplossen: f'(x) = 3600 – 240x + 3x² = 0.
Je vindt: x = 20  V  x = 60. De extremen zijn: max.f(20) = 32000 en min.f(0) = 0.

Voor het buigpunt los je op: f"(x) = –240 + 6x = 0.
Dit levert op: x = 40 en het buigpunt (40, 16000).

Inderdaad zie je bij dit deel van de grafiek alle karakteristieken.