Uitleg

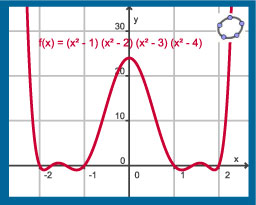
Hier zie je de grafiek van de functie f met
f(x) = (x² – 1)(x² – 2)(x² – 3)(x² – 4)
Werk je de haakjes uit, dan krijg je:
f(x) = x⁸ – 10x⁶ + 35x⁴ – 50x² + 24.

De functie heeft een voorschrift dat bestaat uit een optelling (aftrekking) van machtsfuncties waarvan de exponent een geheel getal groter of gelijk aan 0 is. Je noemt zo'n uitdrukking een veelterm of polynoom. Functie f is een veeltermfunctie. In dit geval spreek je van een achtstegraads functie omdat 8 de hoogte exponent van x is die voorkomt. Er zijn ook acht nulpunten. Meer is onmogelijk, minder kan wel, volgens de hoofdstelling van de algebra.

Om extremen te bepalen ga je differentiëren.
f'(x) = 8x⁷ – 60x⁵ + 140x³ – 100x = 0 geeft hier 7 oplossingen.
Meer is onmogelijk, minder kan wel, volgens de hoofdstelling van de algebra.

Om buigpunten te bepalen stel je de tweede afgeleide gelijk aan 0.
f"(x) = 56x⁶ – 300x⁴ + 420x² – 100 = 0 geeft hier 6 oplossingen.
Meer is onmogelijk, minder kan wel, volgens de hoofdstelling van de algebra.