Uitleg

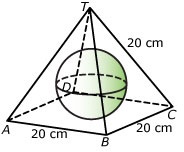
Je ziet hier een regelmatige vierzijdige piramide waarvan alle ribben 20 cm lang zijn. De vraag is hoe groot de grootste bol is die nog juist binnen de piramide past. In het vooraanzicht zie je beter hoe dit bol er uit ziet. Om aan te geven dat A en D recht achter elkaar liggen staat links onder bij de figuur A,D.

Om de straal te berekenen van de grootste bol die nog in deze piramide past, moet je bedenken dat deze bol precies tegen de zijvlakken van de piramide aan gaat komen. Om dat goed te kunnen zien kun je het beste even de aanzichten van piramide met bol bekijken. Het vooraanzicht dat hier is getekend, is hetzelfde als ΔPQT als P het midden van AD en Q het midden van BC is. Dit noem je een doorsnede van de piramide met bol en het vlak door T, P en Q. Hierin is de bol een cirkel die raakt aan PQ, PT en QT. Er zijn dus stralen vanuit het middelpunt M te tekenen die loodrecht op deze zijden staan.
Van ΔPQT weet je alle zijden:
PQ = 20 en PT = QT = $\sqrt{300}$.
Neem je r voor de straal van de bol, dan kun je de gelijkvormigheid van de driehoeken QST en MRT gebruiken om r uit te rekenen.