Uitleg

Bij het aantal combinaties van 3 uit 8 gaat het er eigenlijk om de groep van 8 te verdelen in twee subgroepen, één van 3 en één van 5. Binnen beide subgroepen speelt volgorde geen rol.
Dat kun je heel mooi weergeven in een rooster van 3 bij 5. Elk element van de groep van 8 hoort dan "wel" of "niet" bij het uitverkoren drietal.

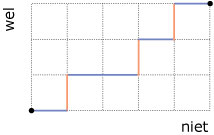
Je ziet hier de mogelijkheid waarin B, E en G wel en de overige niet bij de uitverkoren drie horen.
Alle mogelijke kortste routes van linksonder naar rechtsboven geven het aantal combinaties van 3 uit 8 weer. Het zijn er inderdaad 56, wat je op een handige manier kunt tellen.

Het aantal routes dat in een punt bij elkaar komt is telkens de som van het aantal routes dat in het punt eronder en dat er links naast bij elkaar komt.
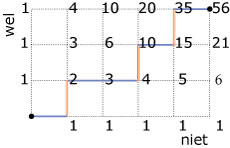Het is de som van de routes van de twee voorgangers.
Je kunt dat in de figuur gemakkelijk natellen als je bedenkt dat je (kortste routes) alleen naar rechts en omhoog kunt bewegen over de roosterlijnen.
Dit telpatroon staat bekend als de driehoek van Pascal.
(Meer hierover bij "Totaalbeeld".)