Theorie
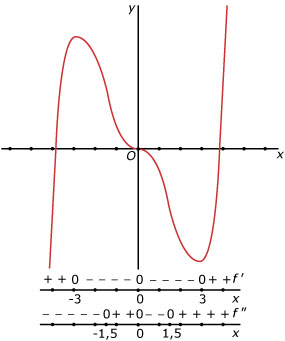
Bij toenemende stijging (daling) of afnemende stijging (daling) kijk je naar de veranderingen van de helling:
- Bij toenemende stijging wordt de helling steeds groter: f' stijgt. De afgeleide van f' is dan positief.
- Bij toenemende daling wordt de helling steeds kleiner (negatiever): f' daalt. De afgeleide van f' is dan negatief.
- Bij afnemende stijging wordt de helling steeds kleiner: f' daalt. De afgeleide van f' is dan negatief.
- Bij afnemende daling wordt de helling steeds groter: f' stijgt. De afgeleide van f' is dan positief.
De tweede afgeleide noteer je als: f" of .
Het punt waarin de helling overgaat van toenemend naar afnemend (of omgekeerd) heet een buigpunt van de grafiek.
Je vindt die buigpunten door naar de extremen van de afgeleide te zoeken.
Dat doe je met behulp van de tweede afgeleide.
