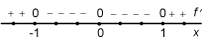Theorie

Extremen berekenen gaat bij een functie, waarvan f(x) het functievoorschrift is, als volgt:

• bepaal met behulp van differentiëren de afgeleide en los op f'(x) = 0, rekening houdend met het domein van de functie;
• bekijk de grafiek van de afgeleide of maak een tekenschema van de afgeleide;
• gaat f'(x) voor x = a over van negatief in positief (en hoort a tot het domein van de functie) dan heeft f een (locaal) minimum van f(a);
• gaat f'(x) voor x = b over van positief in negatief (en hoort b tot het domein van de functie) dan heeft f een (locaal) maximum van f(b).