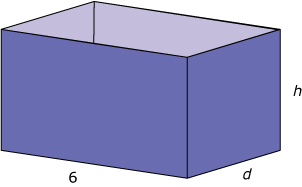
Voorbeeld

Iemand bouwt in zijn schuur een rechthoekige opbergbak met bodem en zonder deksel. De breedte van de bak moet 6 dm worden, meer ruimte is er niet. De inhoud van de bak moet 1 m³ worden. De diepte en de hoogte van de bak kunnen nog variëren.

Bij welke diepte en welke hoogte wordt de totale oppervlakte van de bak minimaal? (Dan zijn waarschijnlijk de materiaalkosten het laagst.)

Antwoord

Noem de diepte d en de hoogte h, beide in dm.
Vanwege de inhoud van 1 m³ = 1000 dm³, geldt: 1000 = 6 · d · h en dus h = $\frac{1000}{6d}$.

Voor de totale oppervlakte A in m² geldt: A = 6d + 12h +  2dh.
Als je nu de eerder gevonden uitdrukking invult in de oppervlakteformule, vind je A = $6d+\frac{2000}{d}+\frac{1000}{3}$.

Van deze functie van d moet je het minimum bepalen. Omdat je een functie van deze vorm nog niet kunt differentiëren, doe je dat met behulp van de grafische rekenmachine. Ga na dat je vindt: d ≈ 18,26. De bijbehorende waarde voor de hoogte kun je dan ook wel berekenen.