Voorbeeld
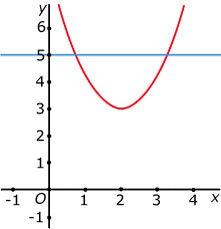
Gegeven is de kwadratische functie `f(x) = 2(x - 2)^2 + 3` en de lijn `y = 5`.
De grafiek van deze kwadratische functie is een parabool. Bepaal de top en de symmetrieas van deze parabool en de snijpunten met de gegeven lijn.
Antwoord
De top van de parabool lees je uit de formule af: `(2,3)`.
De symmetrieas is een lijn door de top en evenwijdig aan de `y`-as, dus `x = 2`.
Voor de snijpunten moet je oplossen `2(x - 2)^2 + 3 = 5`.
| `2(x - 2)^2 + 3 = 5` | |
| `darr` beide kanten `-3` en `//2` | |
| `(x - 2)^2 = 1` | |
| `darr` beide kanten worteltrekken | |
| `x - 2 = 1` of `x - 2 = -1` | |
| `darr` beide kanten `+ 2` | |
| `x = 3` of `x = 1` |
De snijpunten zijn `(1,5)` en `(3,5)`.
