Kwadratische verbanden

Verkennen

Eerst moet je wat voorkennis uit de Basiswiskunde ophalen.

Opgaven

1. Ga naar

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kwadratische verbanden > Uitleg

   Hier kun je nog even nalezen welke voorkennis over kwadratische verbanden bekend wordt verondersteld.

   Bij welke van de volgende formules is sprake van een kwadratisch verband tussen `x` en `y`?
   1. `y = x^2`
   2. `y = 2(x + 1)^2 - 5`
   3. `y = x^2 + x^3`
   4. `y = x(x - 2)`
   5. `y = x(x - 2) - x^2`


2. De formule `y = -0,5(x - 1)^2 + 4` hoort bij een kwadratisch verband.
   1. Hoe ziet de bijbehorende grafiek er uit? Hoe heet zo'n grafiek en hoe teken je hem?
   2. Welk punt van de grafiek kun je onmiddellijk uit de formule aflezen?


3. Ga naar

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kwadratische vergelijkingen > Uitleg

   Hier kun je nog even nalezen welke voorkennis over kwadratische vergelijkingen bekend wordt verondersteld.

   1. Bekijk de formule uit de voorgaande opgave. Hoe bereken je de snijpunten van deze grafiek met de assen?
   2. Bereken nu de snijpunten met de `x`-as door de bijbehorende kwadratische vergelijking op te lossen.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 3 VWO > Formules en grafieken > Kwadratische functie > Uitleg

Je kunt nu lezen wat een kwadratische functie is en dat een kwadratische functie veel voorkomt bij oppervlakteberekeningen.

Opgaven

4. Bekijk Uitleg 1.
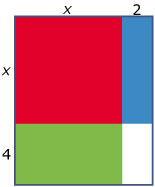
   Bij het vierkant hiernaast worden rechthoekige stroken aangelegd. De zijde van het vierkant is `x`, de breedtes van de rechthoekige stroken is bekend. Je ziet hoe die stroken in drie rechthoeken zijn verdeeld. Samen met het vierkant vormen ze één grote rechthoek.
   1. Leg uit waarom voor de oppervlakte `A` van de grote rechthoek geldt: `A(x) = x^2 + 6x + 8`.
   2. Leg uit waarom voor de oppervlakte `A` van de grote rechthoek geldt: `A(x) = (x + 4)(x + 2)`.
   3. Laat door haakjes uitwerken zien dat beide formules hetzelfde zijn.
   4. Waarom noem je `A` een kwadratische functie van `x`?


5. In de applet in Uitleg 2 kun je met de schuifbalkjes werken.
   1. Maak de kwadratische functie `f(x) = 0,5(x + 1)^2 + 2`.
      Leg uit waarom deze functie een minimum heeft van 2 voor `x = -1`.
   2. Wat is het verschil tussen het minimum en de top van de grafiek?
   3. Maak de kwadratische functie `f(x) = -0,5(x - 1)^2 + 3`.
      Heeft deze functie een maximum of een minimum? Leg uit waarom.
   4. Schrijf het maximum en de bijbehorende `x`-waarde op.

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 3 VWO > Formules en grafieken > Kwadratische functie > Voorbeeld 1

Bekijk Voorbeeld 1. Je ziet nog eens hoe je vanuit gegeven formules snijpunten berekend.

Opgaven

6. Bekijk hoe je de snijpunten berekent van een parabool en een rechte lijn evenwijdig aan de `x`-as waarvan de formules gegeven zijn.
   Doe dit zelf bij deze gegevens:
   1. `f(x) = 2(x - 2)^2 + 3` en `y = 7,5`
   2. `f(x) = -0,5(x - 3)^2 + 1` en `y = 2`
   3. `f(x) = x^2 - 4` en `y = 12`
   4. `f(x) = -(x + 3)^2` en `y = -25`


7. Gegeven is de kwadratische functie `f` met `f(x) = -2(x - 5)^2 + 10`.
   1. Bepaal de extreme waarde van `f`.
   2. Welke vergelijking heeft de symmetrieas van de grafiek van `f`?
   3. Bereken de snijpunten van de grafiek van `f` met de lijn `y = 6`. Laat de wortels in het antwoord staan.
   4. Bereken de snijpunten van de grafiek van `f` met de `x`-as in één decimaal nauwkeurig.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 3 VWO > Formules en grafieken > Kwadratische functie > Voorbeeld 2

Bekijk Voorbeeld 2.

Opgaven

8. Je ziet een parabool met een formule er naast. Je kunt hier nalezen hoe je zelf zo'n formule kunt opstellen.
   1. Waarom is het in dit voorbeeld echt nodig dat je de top van de parabool kunt aflezen?
   2. Vervolgens wordt het punt `(0,1)` gebruikt om de formule af te maken. Je had daarvoor ook het punt `(4,1)` kunnen gebruiken. Laat zie dat dit hetzelfde resultaat oplevert.
   3. Had je ook het punt `(0,5; 2)` kunnen gebruiken? Leg uit waarom wel of niet.


9. Oefenen nu met de applet samen met een medeleerling.
   Laat de ander een parabool maken (waarbij de top en minstens één ander punt goed is af te lezen) en probeer dan vervolgens zelf de juiste formule te maken. In de applet kun je meteen zien of je het goed hebt gedaan...

Voorbeeld 3

www.math4all.nl > MAThADORE-basic HAVO/VWO > 3 VWO > Formules en grafieken > Kwadratische functie > Voorbeeld 3

Bekijk Voorbeeld 3.

Opgaven

8. Je ziet hoe het vinden van een grootste oppervlakte wordt aangepakt door eerst één variabele te kiezen.
   1. Wat stelt de variabele `b` hier voor?
   2. Hoe wordt de formule voor de oppervlakte `A(b)` nu gevonden?
   3. Maak zelf de grafiek van `A(b)`. Maak eerst een geschikte tabel.
   4. Welke maximale waarde heeft `A`?


9. In Voorbeeld 3 had je ook kunnen beginnen door `BC = p` te kiezen.
   1. Welke uitdrukking had je dan voor `AB` gevonden?
   2. Welke formule voor `A(p)` zou je dan hebben gekregen?
   3. Laat met behulp van een grafiek van `A(p)` zien, dat je dezelfde maximale waarde voor `A` zou hebben gevonden.

Oefenen

10. Bepaal van de volgende kwadratische functies het maximum of minimum.
    1. `f(x) = 2(x - 4)^2 + 5`
    2. `g(x) = -0,01(x - 10)^2 + 1,5`
    3. `h(x) = 5 - 0,3x^2`
    4. `k(x) = (x + 10)^2 - 25`


11. Stel de formule op van de parabool met de volgende gegevens.
    1. De parabool heeft top `(1,5; -3)` en gaat door `(0,2)`.
    2. De parabool heeft top `(15; 400)` en gaat door `(5,100)`.
    3. De parabool gaat door `(2,0)` en `(6,0)` en heeft een maximum van 3.


12. Los de volgende vergelijkingen op (laat als wortels niet mooi uitkomen deze in het antwoord staan):
    1. `0,5x^2 - 100 = 23`
    2. `2(x - 5)^2 = 288`
    3. `(x + 6)^2 + 35 = 84`
    4. `2(x + 10)^2 - 25 = 75`
    5. `2(x + 10)^2 - 25 = 76`
    6. `25 - 0,1(x - 10)^2 = -15`

Toepassen

Geef bij elk van de volgende opgaven een uitgebreide toelichting.

14. Iets met een landje.


15. Baan van een bal.
16. Boog van een brug.

Antwoorden