Fragmenten
menu-onderdelen
Fragmenten

Niets is zeker tot het bewijs is geleverd...
Maar wat is een bewijs?
En hoe kun je dat leveren zonder vormfouten te maken?

Inhoud:

Zeker willen zijn...

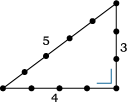
De beroemde 3,4,5-steek is al duizenden jaren bekend en al heel lang in gebruik.
Het plaatje laat zien hoe, vaak met een touw met knopen.
Gek genoeg is een 3,4,5-driehoek rechthoekig, maar bijvoorbeeld een 4,5,6-driehoek niet. Waarom is dat zo?
Wanneer krijg je wel een rechte hoek en wanneer niet?
Wat is er zo bijzonder aan de getallen 3, 4 en 5 dat drie lijnstukken van deze lengte een rechte hoek kunnen vormen?

Is het een typisch menselijke eigenschap dat er altijd wel personen zijn die zichzelf dit soort vragen stellen? Niet iedereen doet het, maar in alle tijden zijn er wel mensen die het naadje van de kous willen weten. En dus niet genoeg hebben aan voorbeelden.
En wanneer weet je iets nou echt zeker?
Dan moet er wel een keihard bewijs worden geleverd.
Dat is waar wiskunde nu eigenlijk over gaat: echt iets zeker weten.

Wiskunde is een woord uit het Nederlands dat afkomstig is van 'wis en zeker' of zoals je tegenwoordig zegt: 'zeker en vast', of 'zo zeker als een huis'. De Zuid-Nederlandse wiskundige Simon Stevin is de bedenker van deze term.
De rest van de wereld zegt 'mathematics' of 'mathématique' of 'Mathematik' of een andere variant van het Griekse 'mathematikoi' waarmee de naaste volgelingen van Pythagoras werden aangeduid.

Een vermoeden onderzoeken

Een manier om de 3,4,5-steek verder te onderzoeken is uitgaan van een rechte hoek en twee gegeven benen van die rechte hoek. Je zoekt dan een manier om het lijnstuk tussen de eindpunten van die benen te berekenen. In de Oudheid lag het voor de hand om voor de lengte van die benen gehele (positieve) getallen te nemen, andere getallen 'bestonden' nog niet. Het te berekenen lijnstuk heette 'hypothenusa'.

Door meer gevallen te proberen ontdek je de regelmaat:
de vierkanten op de benen van een rechthoekige driehoek hebben samen dezelfde oppervlakte als het vierkant op de hypothenusa.

Op deze manier regelmaat vinden heet inductief redeneren:
vanuit veel voorbeelden trek je een conclusie.
Dat is een belangrijke manier van werken want de hele wetenschap is erop gebaseerd. Alleen voor wiskundigen is het niet genoeg.

Een mooi voorbeeld is de formule n2 + n + 41 voor priemgetallen.
Hij klopt voor n = 0: het getal 41 is een priemgetal.
Hij klopt voor n = 1: het getal 43 is een priemgetal.
Hij klopt voor n = 2: het getal 47 is een priemgetal.
Hij klopt voor n = 3: het getal 53 is een priemgetal.
Hij klopt voor n = 4: het getal 61 is een priemgetal.
En blijf maar proberen...
De formule lijkt wel altijd te kloppen.

Maar. hij klopt natuurlijk niet voor n = 41. (Waarom niet?).
Bij (inductief) redeneren door proberen gaat deze formule heel lang goed. Je krijgt het vermoeden dat hij altijd een priemgetal oplevert. Maar toch is er opeens een waarde voor n waarvoor hij niet meer werkt. En dat is ook precies het gevaar van redeneren door proberen: je bent nooit uitgeprobeerd. En tot je uitgeprobeerd bent weet je niet zeker of het resultaat altijd geldig is.

Altijd waar?

Als je zeker wilt zijn dat een bepaald vermoeden altijd waar is, heb je een bewijs nodig: een redenering die iedereen overtuigt. En dat is vaak nog helemaal niet zo eenvoudig.

Neem als voorbeeld het vermoeden:
de vierkanten op de benen van een rechthoekige driehoek hebben samen dezelfde oppervlakte als het vierkant op de hypothenusa.

Voor dit vermoeden bestaat een groot aantal bewijzen. De animatie hiernaast is een bewijs zonder tekst. Hij is gebaseerd op het feit dat de oppervlakte van een parallellogram niet verandert zolang basis en hoogte niet veranderen. Daarom blijven de oppervlakten van de groene en de rode vierhoek telkens hetzelfde. En omdat ze het blauwe vierkant precies kunnen bedekken zijn ze samen even groot als dat blauwe vierkant.

Maar hoe overtuigend is zo'n bewijs?
In dit geval moet je weten wat een parallellogram is. Verder moet je weten dat de oppervlakte daarvan niet verandert zolang basis en hoogte niet veranderen. Maar hoe zeker weet je dat? Weet je wel wat basis en hoogte van een parallellogram zijn?
Je ziet dat het bewijs voorkennis veronderstelt.
Die voorkennis moet dan ook wel zeker zijn, want anders is het bewijs op drijfzand gebouwd. Dus die voorkennis moet eerst bewezen worden. En misschien is voor het bewijs van die voorkennis wel weer voorvoorkennis nodig, enzovoort.

Stilzwijgende aannames

Als je een bewijs levert dan stel je een redenering op die iedereen overtuigt. Maar waar begin je?
Je begint bij zaken waarvan onomstotelijk vaststaat dat ze waar zijn, waarvan iedereen aanneemt dat ze waar zijn.
Maar zijn die er wel?

Euklides dacht zo'n 2300 jaar geleden dat ze er voor de wiskunde in ieder geval wel waren. Hij was de eerste (voor zover we weten) die in zijn boek 'Stoicheia' ('De elementen') een complete theorie voor de wiskunde opbouwde.
Daarbij gebruikte hij 23 definities van basisbegrippen zoals 'punt', 'lijn', 'lijnstuk', 'vlak', 'hoek', 'afstand', 'cirkel', enzovoorts. Iedereen weet wel wat die begrippen inhouden, zo redeneerde Euklides, dus die nemen we als uitgangspunt.
Daarnaast gebruikte hij precies 5 axioma's, dat zijn 5 uitspraken waarvan wordt aangenomen dat ze waar zijn. Die stilzwijgende aannames worden niet bewezen, ze zijn het fundament van de theorie.
De vijf postulaten (axioma's) van Euclides zijn:

  1. Het is mogelijk om van elk punt naar elk ander punt een lijnstuk te tekenen.
  2. Het is mogelijk om elk lijnstuk te verlengen tot een (rechte) lijn.
  3. Het is mogelijk met elk middelpunt en met elk lijnstuk als straal een cirkel te tekenen.
  4. Alle rechte hoeken zijn aan elkaar gelijk.
  5. Als een rechte lijn twee andere rechte lijnen snijdt en de binnenhoeken aan dezelfde kant zijn kleiner dan twee rechte hoeken, dan snijden de lijnen elkaar aan die kant.

Verder gebruikte hij om te kunnen redeneren 9 algemene inzichten, waaronder:
1. Dingen, gelijk aan hetzelfde, zijn ook aan elkaar gelijk.
2. En als men bij gelijke dingen gelijke voegt, zijn de totalen gelijk.
3. En als men van gelijke dingen gelijke afneemt, zijn de resten gelijk.
7. En dingen die op elkaar passen zijn gelijk.
8. En het geheel is groter dan het deel.

Hier vind je de volledige lijst in Nederlandse vertaling.

Op basis van al deze aannames (die overigens honderden, zelfs duizenden jaren onaantastbaar leken) bouwde Euklides een samenhangende theorie op voor alle wiskunde, maar vooral voor de vlakke meetkunde. Beslist een enorme prestatie.
Er waren echter ook nadelen en problemen, die feitelijk vanaf het begin van de theorie ook wel duidelijk waren:

In latere eeuwen, na 1800, werden er andere axiomastelsels voor delen van de wiskunde voorgesteld. Bijvoorbeeld het axiomastelsel van Peano voor de natuurlijke getallen, de axiomastelsels voor niet-euclidische meetkundes van Bolya en Lobachevsky.
Steeds gaat het om een samenhangend stelsel van niet-strijdige stilzwijgende aannames, een soort van basiswetboek voor (een deel van) de wiskunde...

Een bewijs, geen vormfouten maken

Na het vaststellen van het fundament (het basiswetboek) voor de wiskunde, moest Euklides echt elke in onze ogen wellicht flauwe uitspraak daaruit afleiden. Dat noem je een bewijs. De uitspraak was in feite een vermoeden, dat pas een echte onwrikbare stelling werd nadat het bewijs was geleverd.

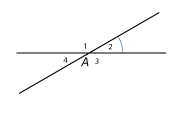Stel je bijvoorbeeld maar eens de uitspraak "overstaande hoeken zijn altijd gelijk" voor.
Dit lijkt wel heel erg waar als je naar de figuur kijkt. Maar daarmee bewijs je niets, gezichtsbedrog komt veel voor.
Eigenlijk is deze uitspraak nog een vermoeden.
Pas als je hebt laten zien hoe hij uit de definities, de axioma's en de algemene aannames kan worden afgeleid, heb je een bewijs geleverd. En dan pas spreek je van een stelling.

Stelling:
Bij twee snijdende rechte lijnen zijn overstaande hoeken altijd gelijk.

Bewijs:
De hoeken A1 en A3 zijn overstaande hoeken.
Hoek A1 vormt samen met A2 een gestrekte hoek (rechte lijn).
Hoek A3 vormt samen met A2 een gestrekte hoek (rechte lijn).
Alle gestrekte hoeken zijn even groot.
Zowel hoek A1 als hoek A3 zijn een gestrekte hoek min hoek A2 en dus ook even groot.
Q.e.d.

Ga nog maar eens nauwkeurig na welke axioma's en welke algemene aannames er worden gebruikt. Per slot mogen er geen vormfouten zijn gemaakt.