|
Wat is wiskunde nou eigenlijk, wat doen wiskundigen?
En waar slaat in dit verband deze titel op? Inhoud: |
Inleiding

Eeuwen en eeuwen kijkt de mens nieuwsgierig naar zijn wereld.
Hij wil wat hij ziet met anderen uitwisselen; er ontstaat taal.
Taal waarmee hij begrippen als vorm, aantal, plaats en tijd kan uitdrukken.
Voordat er van wiskunde echt sprake was waren woorden die bij deze begrippen hoorden al doodgewoon:
- bij vorm: punt, lijnstuk, driehoek, vierkant, cirkel, kubus, balk, piramide, kegel, bol, cilinder, ...
- bij aantal: de getallen 1, 2, 3, 4, ...
- bij plaats: voor, achter, links van, hoger dan, afstand, ...
- bij tijd: voor, na, dagen, jaren
Maar het gebruiken van deze woorden is geen wiskunde ...
Je spreekt pas over wiskunde als je er mee redeneert, als je ze gebruikt om problemen mee op te lossen.
Bijvoorbeeld:
Je wilt een rechthoekig stuk land afzetten, makkelijk bij het oogsten.
Hoe zorg je er dan voor dat je echte rechte hoeken krijgt?
Dergelijke problemen ontstonden vooral toen mensen zich gingen vestigen en dorpen en steden
gingen bouwen, zo'n 5000 jaar geleden.
En toen ontstond ook de eerste wiskunde.
Heel praktisch: gewoon vertellen hoe je bijvoorbeeld zo'n rechte hoek maakt.
De manier van werken doorgeven van ouder op kind.
Geen wiskundige theorie, dat kwam later,
duizenden jaren later ...
Een rechte hoek maken
En hoe maakte je dan een rechte hoek?
De stelling van Thales gebruiken
Natuurlijk wist niemand voor 600 v.Chr. wat de stelling van Thales was.
Maar wel wisten de bouwmeesters van het Oude Egypte en van Mesopotamië dat
een driehoek op een middellijn van een cirkel en met de derde hoek op de cirkel
een rechte hoek had.
De Oudgriekse wijsgeer Thales van Milete haalde deze kennis naar de Griekse wereld. En die gingen zich afvragen waarom dat nou zo was ...
De stelling van Pythagoras gebruiken
De beroemde 3,4,5-steek was al duizenden jaren geleden bekend. En hij is nog heel lang gebruikt. Het plaatje laat zien hoe hij werd gebruikt, vaak met een touw met knopen.
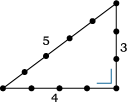
Gek genoeg is een 3,4,5-driehoek rechthoekig,
maar bijvoorbeeld een 1,2,3-driehoek niet.
Waarom is dat zo?
Al heel lang geleden werd ontdekt wat veel later de stelling van Pythagoras zou gaan heten.
En die stelling veranderde de wereld ...
Het begin van de wiskunde

Kennis zoals die hiervoor is beschreven was al in de vroege Oudheid bekend.
De eerste stedelijke beschavingen (Egypte en Mesopotamië en het oude China) gebruikten ze al.
Ze werd vanaf zeker moment te waardevol om alleen mondeling te worden doorgegeven.
Dus werden er voorbeeldberekeningen op schrift gesteld.
Bekijk het kleitablet uit Mesopotamië maar eens, herken je de cirkel bovenaan?
De bijbehorende tekst is in spijkerschrift en gaat over de omtrek en de oppervlakte van de cirkel.
In Egypte was Ahmes de schrijver van de zogenaamde Rhind-papyrus.
Deze payrus is geschreven in ongeveer 1650 v.Chr.
Ahmes beweerde daarop de wiskundige kennis van ongeveer 1850 v.Chr. vast te hebben gelegd.
De oude Egyptenaren konden problemen oplossen die zijn te vergelijken
met het oplossen van een lineaire vergelijking met één onbekende.
Zij gebruikten daarbij geen symbolen, maar beschreven het probleem en de oplossing in woorden.
Ze maakten alleen voorbeelduitwerkingen, die lieten zien hoe je te werk moest gaan.
Maar ook toen al werd een belangrijk principe van de wiskunde duidelijk: Je spreekt alleen over modellen, niet over de veel te ingewikkelde werkelijkheid.
- Een piramide was een ideale piramide, niet zo'n bouwsel van steen met al zijn uitsteeksels en butsen.
- Een cirkel was een ideale cirkel en niet zomaar een onvolmaakt rondje.
- Een driehoek was een ideale vlakke driehoekige figuur, niet een driehoek op het aardoppervlak.
Vooral de Oude Grieken raakten hier na 600 v.Chr. van doordrongen. Plato meende zelfs dat deze 'wereld van ideale vormen' de echte wereld was en onze werkelijkheid maar een slechte weerspiegeling ervan.
Met Thales en later Pythagoras en zijn volgelingen ontstond de eerste echte wiskunde.
Zij meenden dat de wereld was te beschrijven met getallen en vormen.
En zij zochten als eersten naar het waarom van bepaalde methoden uit de Oudheid.
Zij probeerden te beredeneren waarom iets waar was.
Zij ontdekten het bewijs, onder andere van de stelling van Pythagoras.
Later meer over bewijzen ...
Het getal π
Dat er bij dergelijke vereenvoudigingen verrassende ontdekkingen horen laat het getal π zien.
Wat is het getal π?
Wagenmakers weten al heel lang dat de omtrek van een wiel iets meer dan 3 keer zo groot is dan de diameter (middellijn).
Dat 'iets meer' was in de praktijk geen probleem als je de ijzeren rand om het wiel moest maken.
Maar voor wiskundigen is een uitspraak als:
"De omtrek van een cirkel is iets meer dan 3 keer zo groot als de diameter"
veel te vaag.
Zij willen al heel lang weten hoeveel keer dat precies is! Zij noemen het getal dat zegt met hoeveel je de diameter van een cirkel moet vermenigvuldigen om de omtrek te krijgen π. En gek genoeg is dat getal niet precies te berekenen!
Dus het vereenvoudigen van een wiel tot een zuiver ronde ideale cirkel levert ineens
een verrassend resultaat: een getal dat niet gewoon geheel of een deling (verhouding) van twee
gehele getallen is.
Het vinden van een benadering van π in zoveel mogelijk decimalen houdt wiskundigen tot op de dag van vandaag bezig ...
Een wereld van modellen
Wiskundigen houden zich bezig met modellen.
Modellen die ontstaan door de situatie van alle voor het probleem nutteloze franje te ontdoen en dan alle bruikbare begrippen nauwkeurig vast te leggen. Binnen zo'n model kunnen ze nauwkeurige uitspraken doen.
Denk nog maar eens aan het getal π.
Praktijkprobleem:
Hoeveel keer de diameter is de omtrek van een rond wiel?
Model:
Aannames:
de begrippen punt, lijnstuk en lengte zijn bekend.
Definities (afspraken):

- de afstand tussen twee punten is de lengte van het lijnstuk ertussen
- een cirkel is de verzameling van alle punten die op dezelfde afstand (de straal) van een vast middelpunt liggen
- de omtrek van een cirkel is de lengte van het lijnstuk dat ontstaat als je hem doorknipt en recht trekt
- de diameter van een cirkel is twee keer zo lang als de straal
- de omtrek gedeeld door de diameter is het getal π
Alleen binnen zo'n model heeft het zoeken naar de grootte van het getal π enige betekenis. Maar heb je dan π gevonden, kun je die kennis weer toepassen. Bijvoorbeeld bij het berekenen van de lengte van het wegdek van een rotonde ...




