Spiralen

Een praktische opdracht voor de tweede fase vwo, wiskunde B

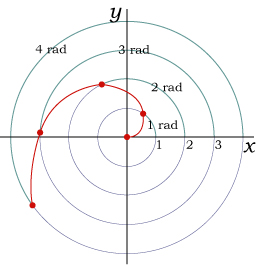De spiraal van Archimedes is een kromme waarvan de hoek naar een bepaald punt een veelvoud is van de afstand van dat punt tot de oorsprong: r = a · θ.
Bekijk de figuur.

• Als de grafische rekenmachine in de mode "pol" (van "polar" omdat je dan werkt met poolcoördinaten), kun je een dergelijke formule invoeren en de spiraal zien ontstaan. Bekijk eventueel het practicum Krommen op de TI83. Maak zo zelf een aantal spiralen. Licht je werkwijze toe.
• Je kunt ook spiralen maken van de vorm r = b + a · θ. Leg uit wat het verschil is als b geen 0 is.
• Probeer nu heel nauwkeurig een constructiebeschrijving van een Archimedische spiraal te maken. (Als je beschikt over het programma "GeoGebra" voor vlakke meetkunde, dan kun je deze constructie ook naspelen.)

Je bent eigenlijk bij krommen gewend om niet met poolcoördinaten te werken, maar met een parametervoorstelling van de vorm x(t) = ... en y(t) = ....
Je kunt een vlakke kromme in poolcoördinaten omzetten naar deze parametervorm.

• Geef een parametervoorstelling van de Archimedische spiraal. Laat duidelijk zien hoe je hem uit de gegeven vorm r = b + a · θ kunt afleiden
• Laat door middel van berekeningen zien dat de spiraal de assen niet loodrecht snijdt.
• Toon aan dat er wel punten te vinden zijn waarin de raaklijn aan de spiraal evenwijdig is aan één der assen.
• Een halve lijn vanuit de oorsprong van snijdt de spiraal achtereenvolgens in O, A, B, C, etc. Kun je iets zeggen over de lengtes van de lijsntukken OA, AB, BC, etc.? Ontdek je regelmaat?

Behalve Archimedische spiralen bestaan er ook andere spiralen, bijvoorbeeld de logaritmische spiraal. Ook bij andere soorten spiralen kun je vergelijkbare berekeningen doen en een constructiebeschrijving maken. Een animatie in GeoGebra vergroot de feestvreugde natuurlijk!

De opdracht

• Werk de gestelde opdrachten over de Archimedische spiraal zorgvuldig uit.
• Probeer de constructiebeschrijving te vertalen in een animatie in GeoGebra.
• Zoek informatie over de achtergronden van de Archimedische spiraal: waarom was hij in de Oudheid belangrijk, wat kon men er mee doen?
• Zoek enkele voorbeelden van spiralen in de natuur en ga na over welke soort spiraal het dan gaat.
• Kies nog minstens één andere soort spiraal dan de Archimedische spiraal en voer ook daarvoor vergelijkbare berekeningen uit. Maak weer een constructiebeschrijving en zet die om in een animatie in GeoGebra. Zoek informatie over de functie van die spiralen. Kun je bijvoorbeeld ook een spiraal van buiten naar binnen laten lopen?
• Maak van al je resultaten een leesbare uitwerking. Geef daarin met duidelijke tekeningen en berekeningen tekst en uitleg over de verschillende soorten spiralen.