Parameterkrommen met de TI-83/84
De TI-83/84 kan krommen tekenen die worden gegeven door x als functie van t en y als functie van t.
De variabele t heet de parameter van de kromme, je kunt hem opvatten als de 'tijd'. Op elk tijdstip t kun je met behulp van de functies x(t) en y(t) berekenen op welke plaats (x, y) het punt dat de kromme doorloopt zich bevindt. Ook kan de TI-83/84 hellingsgetallen berekenen in elk punt van de kromme.
Een andere manier om krommen te beschrijven is met behulp van poolcoördinaten. Daarover gaat het laatste deel van dit practicum.
Loop eerst het practicum: 'Functies' door.
Inhoud
Een parameterkromme tekenen
Stel je voor dat je de kromme K wilt tekenen gegeven door:
(x(t), y(t)) = (5·sin(t)), 5·sin(2t)), met t lopend van 0 tot en met 2p.
Je zet dan eerst de rekenmachine in de juiste 'Mode':
- [Mode] en kies voor Radian (voor het werken in radialen) en Par (voor Parametric curve)
- Via [2nd] [Mode] verlaat je dit scherm
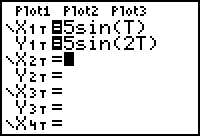 Vervolgens ga je via [ Y= ] de kromme invoeren.
Vervolgens ga je via [ Y= ] de kromme invoeren.
Als je op die knop drukt krijg je het scherm hiernaast, meestal zonder ingevoerde kromme, maar er kan ook nog werk van een vorige gebruiker in staan. Vervolgens voer je de twee functies x(t) en y(t) in, net zoals je dat bij gewone functies doet.
Ook nu werk je met [X,T,q,n] om de variabele (de t) in te voeren, hier levert dat een T op.
In het scherm hiernaast zie je de kromme op de juiste wijze ingevoerd.
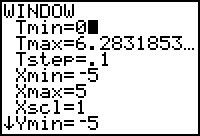 Voordat je de grafiek gaat bekijken moet je eerst de vensterinstellingen goed maken.
Dat doe je (net als bij functies) via [WINDOW].
Het scherm dat je dan krijgt begint met de in te stellen waarden voor T en vervolgens kun je de juiste waarden voor X en Y gaan instellen. In het scherm hiernaast zie je geschikte instellingen voor de gegeven kromme. Je ziet, dat de stapgrootte voor t is ingesteld op 0,1. Je kunt ook kleinere stappen maken, maar dan duurt het tekenen van de kromme langer. Maak je daarentegen hele grote stappen, dan worden er maar weinig punten van de kromme berekend, die dan worden verbonden op een zodanige manier dat je de kromme niet herkent!
Voordat je de grafiek gaat bekijken moet je eerst de vensterinstellingen goed maken.
Dat doe je (net als bij functies) via [WINDOW].
Het scherm dat je dan krijgt begint met de in te stellen waarden voor T en vervolgens kun je de juiste waarden voor X en Y gaan instellen. In het scherm hiernaast zie je geschikte instellingen voor de gegeven kromme. Je ziet, dat de stapgrootte voor t is ingesteld op 0,1. Je kunt ook kleinere stappen maken, maar dan duurt het tekenen van de kromme langer. Maak je daarentegen hele grote stappen, dan worden er maar weinig punten van de kromme berekend, die dan worden verbonden op een zodanige manier dat je de kromme niet herkent!
Nu kun je via [GRAPH] de kromme tekenen.
Er ontstaat een mooie 'liggende acht'.
Mogelijk is de kromme niet helemaal gesloten. Kies dan voor t waarden van 0 tot bijvoorbeeld 10 (dus iets meer dan 2p).
Met [TRACE] kun je over de kromme lopen.
Je gaat er dan met 'tijd'stappen van 0,1 (die was immers ingesteld) overheen. De bijbehorende waarden voor t, x en y komen in beeld.
Experimenteer maar eens even met andere instellingen voor t.
Oefen het tekenen van krommen met de TI-83/84.
Zoek voorbeelden van krommen in je wiskundeboek.

Hellingsgetallen bij parameterkrommen
Je hebt de kromme K: (x(t), y(t)) = (5·sin(t)), 5·sin(2t)), met t lopend van 0 tot en met 2p bekeken in het voorgaande deel.
Zorg ervoor dat deze kromme weer in beeld komt.
Bij elk punt van deze kromme kun je je afvragen welke helling de raaklijn aan de kromme heeft.
Deze helling wordt voorgesteld door dy/dx.
Je vindt die helling door [2nd][TRACE] in te tikken (je gebruikt het CALC-menu voor krommen) en dy/dx te kiezen. Vervolgens loop je met de cursor naar het gewenste punt of je tikt de gewenste waarde voor t in.
Ook kun je je afvragen met welke snelheid de kromme wordt doorlopen in een bepaald punt. Daarvoor gebruik je de verandering van x die van y in dat punt, dus x'(t) en y'(t). Deze veranderingen heten op de rekenmachine dx/dt en dy/dt. Ook deze waarden vind je via het CALC-menu.
De snelheid waarmee het punt de kromme doorloopt voor t = 0 bereken je zo:
- Bepaal dx/dt en dy/dt voor t = 0
- Bereken nu de snelheid v(0) uit:
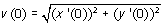
Je vindt bij de gegeven kromme: v(0) = 11,18 eenheden per tijdseenheid (afgerond op twee decimalen).
Bekijk ook de hellingsgetallen en bereken de doorloopsnelheid in andere punten van deze kromme.
Waar gaat het doorlopen het snelst?

Krommen in poolcoördinaten
Een andere manier om een kromme te beschrijven is met zogenaamde poolcoördinaten.
Daarbij werk je in een x,y-assenstelsel, maar geef je een punt P van een kromme weer door een functie van de vorm r = f(q), waarin q de hoek is die het lijnstuk OP met de positieve x-as maakt.
Bekijk het plaatje maar eens.
Een driebladige bloem krijg je met r = 8·sin(3q).
Je voert die formule zo in:
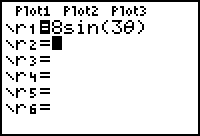
- Stel de machine via [Mode] in op Pol (polar curve). Zorg er voor dat hij ook op radialen staat ingesteld.
- Open het [ Y= ]-scherm en voer de gewenste formule in.
Gebruik weer [X,T,q,n] voor de variabele. Je krijgt automatisch het teken q.
- Stel het venster goed in. In dit geval laat je q van 0 tot 2p lopen en X en Y van –10 tot 10.
- Met [GRAPH] krijg je de kromme te zien.
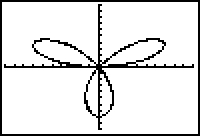 Ook nu kun je met [TRACE] over de kromme lopen, met [ZOOM] inzoomen en uitzoomen en met het CLAC-menu hellingsgetallen laten berekenen in punten van de kromme.
Ook nu kun je met [TRACE] over de kromme lopen, met [ZOOM] inzoomen en uitzoomen en met het CLAC-menu hellingsgetallen laten berekenen in punten van de kromme.
Experimenteer met krommen in poolcoördinaten.
Hoe maak je bijvoorbeeld een achtbladige bloem?

 Math4all
Math4all
 Voordat je de grafiek gaat bekijken moet je eerst de vensterinstellingen goed maken.
Dat doe je (net als bij functies) via [WINDOW].
Het scherm dat je dan krijgt begint met de in te stellen waarden voor T en vervolgens kun je de juiste waarden voor X en Y gaan instellen. In het scherm hiernaast zie je geschikte instellingen voor de gegeven kromme. Je ziet, dat de stapgrootte voor t is ingesteld op 0,1. Je kunt ook kleinere stappen maken, maar dan duurt het tekenen van de kromme langer. Maak je daarentegen hele grote stappen, dan worden er maar weinig punten van de kromme berekend, die dan worden verbonden op een zodanige manier dat je de kromme niet herkent!
Voordat je de grafiek gaat bekijken moet je eerst de vensterinstellingen goed maken.
Dat doe je (net als bij functies) via [WINDOW].
Het scherm dat je dan krijgt begint met de in te stellen waarden voor T en vervolgens kun je de juiste waarden voor X en Y gaan instellen. In het scherm hiernaast zie je geschikte instellingen voor de gegeven kromme. Je ziet, dat de stapgrootte voor t is ingesteld op 0,1. Je kunt ook kleinere stappen maken, maar dan duurt het tekenen van de kromme langer. Maak je daarentegen hele grote stappen, dan worden er maar weinig punten van de kromme berekend, die dan worden verbonden op een zodanige manier dat je de kromme niet herkent!  Vervolgens ga je via [ Y= ] de kromme invoeren.
Vervolgens ga je via [ Y= ] de kromme invoeren.
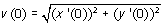

 Ook nu kun je met [TRACE] over de kromme lopen, met [ZOOM] inzoomen en uitzoomen en met het CLAC-menu hellingsgetallen laten berekenen in punten van de kromme.
Ook nu kun je met [TRACE] over de kromme lopen, met [ZOOM] inzoomen en uitzoomen en met het CLAC-menu hellingsgetallen laten berekenen in punten van de kromme.