
De kettingregel

Inleiding
In veel functievoorschriften komen haakjes voor.
Vaak kun je die eenvoudig uitwerken, maar niet altijd.
Met name bij samengestelde functies, zeg maar functies die als een ketting aan elkaar zijn geschakeld, is het uitwerken van haakjes vaak helemaal niet eenvoudig, of zelfs gewoon onmogelijk.
Het differentiëren van dergelijke functies vereist een speciale differentieerregel.
Je leert nu:
- de kettingregel voor het differentiëren van samengestelde functies;
- de kettingregel toepassen.
Je kunt al:
- allerlei soorten functies gebruiken;
- differentiëren met de machtsregel, de constante-regel en de somregel;
- werken met de afgeleide en de tweede afgeleide, onder andere voor het berekenen van extremen en buigpunten.
Verkennen
Bij het lozen van olie op zee ontstaat een zich cirkelvormig uitbreidende olievlek.
De straal R (in meter) van die olievlek hangt af van de tijd t (in uren).
Bijvoorbeeld kan gelden: .
> Waarom is R een samengestelde functie?
> Hoe snel verandert de straal van de olievlek na 3 uur?
> Kun je het antwoord op de vorige vraag met behulp van differentiëren vinden? En hoe dan?
Uitleg
Soms bestaat een functievoorschrift uit in serie geschakelde functies.
Neem bijvoorbeeld S(x) = (2x + 10)3.
Een functiewaarde bereken je nu in twee stappen:
- eerst bereken je g(x) = 2x + 10;
- vervolgens f(g(x)) = (g(x))3.
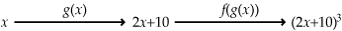
De functie S(x) = (2x + 10)3 = (g(x))3 = f(g(x)) heet een samengestelde functie of kettingfunctie.
Deze kettingfunctie kun je differentiëren door met transformaties te werken:
S'(x) = 3(2x + 10)2 · 2 = 6(2x + 10)2.
Dat gaat echter alleen maar omdat g(x) = 2x + 10 lineair is.
En als de exponent geen geheel getal is kun je ook de haakjes niet uitwerken...
Het differentiëren van een kettingfunctie vereist in het algemeen een speciale differentieerregel: de kettingregel. Om die af te leiden gebruik je de lineaire benadering. Je vindt de afleiding van de kettingregel bij de theorie.
‡
Opgaven
- Gegeven is de functie `h(x) = 3(x - 2)^2 - 2`.
- Waarom is `f` een samengestelde functie? Waaraan herken je dat?
- Ontleed `f(x)` in afzonderlijke schakels.
- Welke invoerwaarden passen bij de functiewaarde 16?
- Deze functie kun je differentiëren zonder eerst de haakjes uit te werken. Laat zien hoe.
-
Schrijf de volgende functievoorschriften als een ketting van afzonderlijke functies.
-
`y = sqrt(x^2 - 1)`
-
`y = 3x^3 + 1`
-
`y = (3x^2 + 2)^4`
-
Gegeven zijn de functies `f(x) = sqrt(x)` en `g(x) = x^2 + 2` met `x >= 0`.
-
Schrijf het functievoorschrift op van `h(x) = f(g(x))`.
-
Kun je `h` differentiëren met behulp van de differentieerregels die je nu kent?
-
Schrijf het functievoorschrift van `k(x) = g(f(x))` zo eenvoudig mogelijk. Kun je deze functie differentiëren met behulp van de differentieerregels die je nu kent?
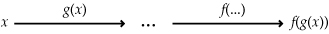
Theorie
Een samengestelde functie is een functie die uit twee of meer in serie geschakelde functies bestaat.
Voor de afgeleide van een samengestelde functie geldt
Differentieerregel 4 (kettingregel):
Als S(x) = f(g(x)) dan is S'(x) = f'(g(x)) · g'(x).
Met behulp van deze regel bewijs je ook de machtsregel voor wortelfuncties:
Als
dan is voor gehele positieve n en x ≠ 0.
In het algemeen geldt:
Differentieerregel 5 (algemene machtsregel):
Als f(x) = xr dan is f'(x) = rxr – 1 voor elke reële waarde van r.
Voor het bewijs van deze differentieerregel moet je eerst leren exponentiële functies en logaritmische functies te differentiëren. Dat komt later.
‡
Voorbeeld 1
Differentieer de functie: S(x) = (x2 + 2x)4.
Antwoord
Deze functie is een samengestelde functie: S(x) = (x2 + 2x)4 = (g(x))4 = f(g(x)).
Hierin is:
- f(g(x)) = (g(x))4 en dus f'(g(x)) = 4(g(x))3
- g(x) = x2 + 2x en dus g'(x) = 2x + 2
De afgeleide van S vind je nu door de kettingregel toe te passen:
S'(x) = f'(g(x)) · g'(x) = 4(g(x))3 · (2x + 2) = 4(x2 + 2x)3 · (2x + 2)
Dit kun je nog schrijven als: S'(x) = (8x + 8)(x2 + 2x)3.
‡
Voorbeeld 2
Met de kettingregel kun je aantonen dat de machtsregel ook geldig is voor wortelfuncties, dus
machtsfuncties met een gebroken exponent. Hij is zelfs geldig voor alle machtsfuncties. Een
paar voorbeelden...
Differentieer de functies:
Antwoord
- Eerst schrijf je f als machtsfunctie:
Vervolgens pas je de machtsregel toe:
Merk op dat het domein van functie f is . Maar bij de afgeleide is x = 0 geen toegelaten waarde.
De grafiek heeft voor x = 0 een verticale raaklijn (zo'n raaklijn heeft geen richtingscoëfficiënt).
- Eerst schrijf je g als machtsfunctie:
Vervolgens pas je de machtsregel toe:
- Eerst schrijf je h als machtsfunctie:
Vervolgens pas je de machtsregel toe:
‡
Voorbeeld 3
Gegeven de functie .
Bereken het hellingsgetal van deze functie voor x = 1.
Antwoord
Eerst even de wortelvorm schrijven als een macht:
Je differentieert f met de kettingregel:
Het gevraagde hellingsgetal is
‡
Opgaven
- Gegeven is de functie `h(x) = (2x^2 + 1)^8`. In Voorbeeld 1 kun je zien hoe je zo'n functie differentieert zonder de haakjes uit te werken.
- Deze functie heeft de vorm `h(x)=f(g(x))`. Schrijf de voorschriften van `f` en `g` op.
- Laat zien dat `h'(x) = 32x(2x^2 + 1)^7`.
- Gegeven zijn de functies `f(x) = x^4` en `g(x) = 2x^3 + 4x`.
- Schrijf het functievoorschrift op van `h(x)=f(g(x))`.
- Bepaal de afgeleide van `h`.
- Schrijf het voorschrift op van de functie `k(x)=g(f(x))`.
- Bepaal de afgeleide van `k`.
- In de Theorie en in Voorbeeld 2 kun je zien hoe je een wortelfunctie differentieert. De machtsregel kun je in het algemeen gebruiken bij elke reële exponent, ook bij gebroken en/of negatieve exponenten. Differentieer de volgende functies. Schrijf de afgeleiden steeds weer zonder gebroken en/of negatieve exponenten.
- `f(x) = 2 sqrt(x)`
- `f(x) = x sqrt(x)`
- `f(x) = root[3](x)`
- `f(x) = 3/(sqrt(x))`
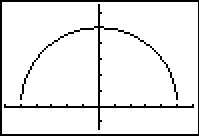 Hier zie je de grafiek van `f(x) = sqrt(25 - x^2)` zoals een grafische rekenmachine hem maakt. Hij lijkt op die in Voorbeeld 3.
Hier zie je de grafiek van `f(x) = sqrt(25 - x^2)` zoals een grafische rekenmachine hem maakt. Hij lijkt op die in Voorbeeld 3.
- Schrijf het domein en het bereik van `f` op. Waaraan zie je dat de grafiek niet helemaal compleet is?
- Bepaal de afgeleide van `f`.
- Hoe kun je met zekerheid concluderen dat deze functie een maximum voor `x=0` heeft?
- De grafische rekenmachine geeft dit aan.
- 5 is de grootste functiewaarde en die waarde zit bij `x=0`.
- `f'(x)=0` alleen als `x=0`.
- `f'(0)=0` en de afgeleide gaat alleen voor `x=0` over van positief naar negatief.
- Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=3`.
Verwerken
- Differentieer de volgende functies.
- `f(x) = (x^2 - 100)^4`
- `g(x) = -5 + (1 - x)^3`
- `H(t) = 25(2 - 4t)^3`
- `y(x) = 2p^2 x - (px + 3)^4`
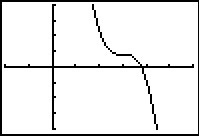 Hier zie je de grafiek van de functie `f(x) = -(2x - 6)^3 + 4`.
Hier zie je de grafiek van de functie `f(x) = -(2x - 6)^3 + 4`.
- De grafiek lijkt dalend voor elke waarde van `x` behalve `x=3`. Toon aan dat dit inderdaad het geval is.
- De raaklijn aan de grafiek van `f` voor `x=2` snijdt de `x`-as in punt `P`. Bereken de coördinaten van `P`.
- Bepaal van de volgende functies de afgeleide:
- `y = root3(x^7)`
- `f(x) = 1/x^3 + 4/x^2 - 3/x + 1`
- `H(p) = (1 - sqrt(p))^3`
- `g(x) = 2x - 5/(1 - x)`
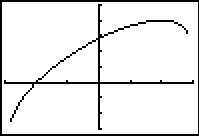 Hier zie je de grafiek van de functie `f(x) = x + sqrt(8 - x^2)`.
Hier zie je de grafiek van de functie `f(x) = x + sqrt(8 - x^2)`.
- Bepaal het domein van `f`.
- Bereken algebraďsch het bereik van `f`.
- Noem de randpunten van de grafiek van `f` respectievelijk `A` en `B`. Voor welke waarde van `x` is het hellingsgetal van de grafiek van `f` gelijk aan dat van lijn `AB`?
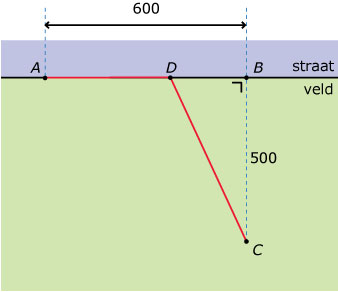 Vanuit punt moet een waterleiding gelegd worden naar punt. Langs de straat bedragen de kosten €30,00 per meter en door het veld €70,00 per meter. De lengte van `AB` is 600 meter en de lengte van `BC` is 500 meter. Er zijn verschillende mogelijkheden om de waterleiding aan te leggen:
Vanuit punt moet een waterleiding gelegd worden naar punt. Langs de straat bedragen de kosten €30,00 per meter en door het veld €70,00 per meter. De lengte van `AB` is 600 meter en de lengte van `BC` is 500 meter. Er zijn verschillende mogelijkheden om de waterleiding aan te leggen:
- langs de straat tot aan punt `B` en vervolgens door het aangrenzende terrein naar punt `C`;
- direct vanuit `A` door het veld, in een rechte lijn naar `C`;
- of een van de vele tussenmogelijkheden: de leiding wordt dan voor een gedeelte langs de straat aangelegd, tot aan punt `D`, en vervolgens vanaf de straat naar punt `C`.
- Hoeveel bedragen de kosten als je voor de eerste mogelijkheid kiest?
- Hoeveel bedragen de kosten als je voor de tweede mogelijkheid kiest?
- Bekijk de derde mogelijkheid. Neem voor de lengte van `BD` de variabele `x`. Druk nu de kosten voor de aanleg van deze waterleiding uit in `x`.
- Hoe moet je de waterleiding aanleggen opdat de kosten minimaal zijn? Bereken de minimale kosten met behulp van de afgeleide.
Testen
- Differentieer de volgende functies
- `f(x) = 6(1 + x^2)^3`
- `y(x) = (1 - 4x)^4 + 5`
- `R(t) = sqrt((15/pi) t)`
- `f(x) = sqrt(10 + 4x^2)`
- `K(p) = 2/(p sqrt(p))`
- `f(x) = x^3 + 2x - 3/(sqrt(x)) + 1/x^2`
- Gegeven is de functie `f(x) = 2x - sqrt(x + 2)`.
-
Als je de grafiek van deze functie op je grafische rekenmachine bekijkt met de standaardinstellingen van het venster, lijkt het wel een rechte lijn te zijn. Wat is het domein van `f`?
- Bepaal de afgeleide van `f`.
- Bereken met behulp deze afgeleide het minimum van `f`.
- Wat is het bereik van deze functie `f`?
- Bereken de hoek waaronder de grafiek van `f` de `y`-as snijdt.


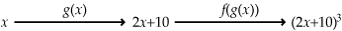
 Hier zie je de grafiek van de functie `f(x) = -(2x - 6)^3 + 4`.
Hier zie je de grafiek van de functie `f(x) = -(2x - 6)^3 + 4`.
 Hier zie je de grafiek van de functie `f(x) = x + sqrt(8 - x^2)`.
Hier zie je de grafiek van de functie `f(x) = x + sqrt(8 - x^2)`.
 Vanuit punt moet een waterleiding gelegd worden naar punt. Langs de straat bedragen de kosten €30,00 per meter en door het veld €70,00 per meter. De lengte van `AB` is 600 meter en de lengte van `BC` is 500 meter. Er zijn verschillende mogelijkheden om de waterleiding aan te leggen:
Vanuit punt moet een waterleiding gelegd worden naar punt. Langs de straat bedragen de kosten €30,00 per meter en door het veld €70,00 per meter. De lengte van `AB` is 600 meter en de lengte van `BC` is 500 meter. Er zijn verschillende mogelijkheden om de waterleiding aan te leggen: