Theorie

Een functie f met voorschrift y = f(x) is

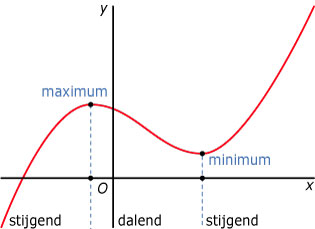
• stijgend als de functiewaarden groter worden bij toenemende x;
• dalend als de functiewaarden kleiner worden bij toenemende x.

• een maximum als hij overgaat van stijgend in dalend en de grafiek aaneengesloten is;
• een minimum als hij overgaat van dalend in stijgend en de grafiek aaneengesloten is.

Er bestaan ook nog soorten stijging (en daling). Er is een:

• constante stijging (daling) als de stijging (daling) voortdurend even sterk blijft;
• toenemende stijging (daling) als de stijging (daling) steeds sterker wordt;
• afnemende stijging (daling) als de stijging (daling) steeds minder sterk wordt.