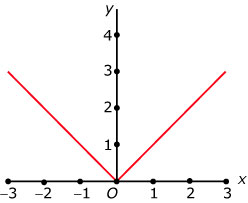
Theorie

De absolute waarde |x| van een getal x is de waarde ervan zonder (min)teken.
Zo is: |3| = 3 en |–3| = 3.
Dit komt omdat beide getallen dezelfde (positieve) afstand tot 0 hebben: ze zijn elkaars tegengestelde. De wiskundige notatie voor de absolute waarde van x is met absoluutstrepen, de meeste rekenmachines gebruiken: abs(x).
De eenvoudigste absoluutfunctie is: y = |x| = $\{\begin{array}{cc}x& \text{als }x\ge 0\\ -x& \text{als }x<0\end{array}$
De grafiek zie je hiernaast.

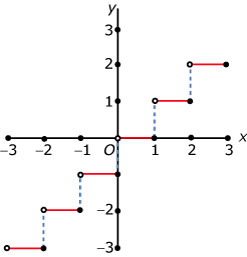Het gehele deel van een getal x is dat getal zonder decimalen. Het gehele deel van 2,913 is hetzelfde als dat van 2,0 en dat van 2,5, namelijk 2.
Het gehele deel van –2,913 is –2.
Hierbij past de zogenaamde entierfunctie of integerfunctie. Deze functie rondt elke x-waarde naar beneden af op een gehele waarde.
Je schrijft: y = int(x).
De grafiek vertoont sprongen, het is een trapgrafiek. Je ziet hem getekend, let goed op de open en de gesloten rondjes.
Het domein van de entierfunctie is $ℝ$.
Het bereik is {..., –3, –2, –1, 0, 1, 2, 3, ...}.