Theorie
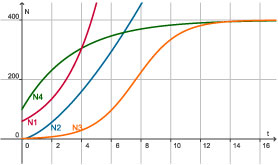
Bij het exponentiële groeimodel hoort een functie van de vorm N1(t) = b · gt of N1(t) = b · ekt of N1(t) = b · 10kt.
(In de figuur is b = 60 en g = 1,5.)
Teken je dergelijke functies op enkellogaritmisch papier dan wordt de grafiek een rechte lijn.
Bij een machtsfunctie als model hoort een voorschrift van de vorm N2(t) = b · tp.
(In de figuur is b = 20 en p = 1,5.)
Van dergelijke functies is de grafiek op dubbellogaritmisch papier een rechte lijn.
Bij een exponentieel geremd groeimodel hoort een functie als N3(t) = .
Kenmerkend voor dit groeimodel is, dat de groei eerst vrijwel exponentieel verloopt, maar op zeker moment (voedselgebrek, te weinig ruimte) afremt. De groeisnelheid die eerst toeneemt, gaat vanaf dat moment afnemen. In dit groeimodel is N = G de horizontale asymptoot en vind je de grootste groeisnelheid bij N(t) = G.
(In de figuur is G = 400, b = 200 en g = 0,5.)
Er zijn tenslotte nog situaties waarin het verschil met een constante waarde exponentieel afneemt. Daarbij hoort een groeimodel van de vorm N4(t) = G + b · gt.
Kenmerkend voor dit groeimodel is dat de groeisnelheid vanaf het begin afneemt.
(In de figuur is G = 400, b = –300 en g = 0,75.)