Toepassingen

Een beroemd probleem uit de Griekse Oudheid stamt uit de "Catoptrica" van Heroon:
Een lichtstraal loopt van punt A naar punt B doordat hij van het oppervlak van een vlakke spiegel wordt teruggekaatst. Aangenomen dat het licht altijd de kortste route neemt, waar raakt het dan de spiegel?

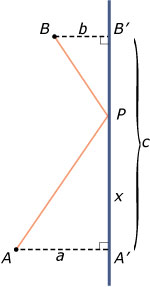Een schets van de situatie laat zien dat hier zowel een aanpak met differentiëren als een aanpak met gelijkvormigheid of goniometrie mogelijk is:

• Met differentiëren:
  De lengte L van de baan van de lichtstraal is:
  L(x) = $\sqrt{a^2+x^2}+\sqrt{b^2+{(c-x)}^2}$.
  Met behulp van L'(x) = 0 vind je de waarde van x waarvoor L minimaal is.
• Met gelijkvormigheid (of tangens):
  ΔAA'P en ΔBB'P zijn gelijkvormig, dus: $\frac{a}{x}=\frac{b}{c-x}$.
  En hieruit kun je x berekenen.