Uitleg

Een blikfabriek maakt onder andere cilindervormige blikken voor de conservenindustrie. Er is veel vraag naar blikken met een inhoud van 1 liter. Voor de fabrikant is het belangrijk dat daar zo min mogelijk blik voor nodig is, dan blijven zijn kosten laag.
Welke afmetingen zal hij zijn literblikken geven?

Eerst een rekenmodel opstellen:
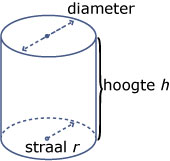
Neem aan dat elk blik zuiver cilindrisch is en dat de benodigde hoeveelheid blik gelijk is aan de totale oppervlakte van het blik. De twee bepalende variabelen zijn dan de straal van (het grondvlak van) het blik r en de hoogte h, neem beide in cm. Het gegeven betreft de inhoud van een blik (1 L = 1000 cm³), de eis betreft de oppervlakte die minimaal moet zijn.
Voor de inhoud van een cilinder geldt: I = πr²h.
Voor de oppervlakte van een cilinder geldt: A = 2πrh + 2πr².
Ga dat na.

Met I = 1000 vind je 1000 = πr²h en dus: $h=\frac{1000}{\pi r^2}$.
Als je nu in de formule voor A deze uitdrukking invult voor h, dan vind je: $A(r)=\frac{2000}{r}+2\pi r^2$.

Met behulp van differentiëren of de grafische rekenmachine vind je nu dat voor x ≈ 5,4 cm en h ≈ 10,8 cm de totale oppervlakte minimaal is.