Theorie

Een functie f is differentieerbaar voor x = a als a tot het domein van f behoort en

$f\text{'}(a)=\underset{h\to 0}{\lim }\frac{f(a+h)-f(a)}{h}$

bestaat. Belangrijk is hierbij dat h zowel positief als negatief moet kunnen zijn: het naar 0 naderen moet zowel van de negatieve als de positieve kant kunnen en hetzelfde getal opleveren!
Dat differentiaalquotiënt is dan de richtingscoëfficiënt van de raaklijn voor x = a aan de grafiek van f. Het komt er dus op neer, dat je de functie voor x = a precies één hellingsgetal moet kunnen geven en een bijpassende vergelijking van de raaklijn moet kunnen opstellen.

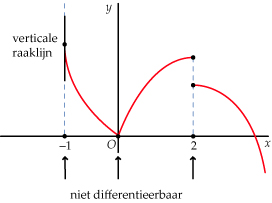
Er zijn verschillende situaties waarin een functie niet differentieerbaar is, terwijl de betreffende x-waarde wel tot het domein van f behoort. Hier zie je daar voorbeelden van. Het gaat om x-waarden waarin de grafiek

• een verticale raaklijn, of
• een knikpunt, of
• een sprong