Voorbeeld

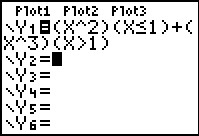
Soms bestaat een functie uit meerdere delen. Bijvoorbeeld:

$f(x)=\{\begin{array}{cc}{x}^2& \text{als }x\le 1\\ x^3& \text{als }x>1\end{array}$

Laat zien dat deze functie niet differentieerbaar is voor x = 1.

Antwoord

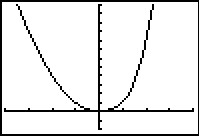
De grafiek van f vertoont bij x = 1 geen sprong, want zowel 1² = 1 als 1³ = 1.
De afgeleide is:

$f\text{'}(x)=\{\begin{array}{cc}2x& \text{als }x\le 1\\ 3x^2& \text{als }x>1\end{array}$

Bekijk je nu het punt (1, 1) dan zie je dat het hellingsgetal 2 wordt als je van links naar x = 1 nadert, terwijl het hellingsgetal 3 wordt als je van rechts naar x = 1 gaat.

Omdat beide hellingen verschillend zijn, is er sprake van een knikpunt en is f niet differentieerbaar voor x = 1.