Voorbeeld

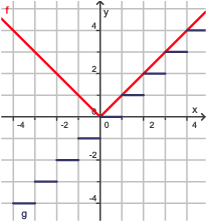
Twee bijzondere functies zijn de absoluutfunctie f(x) = |x| en de integerfunctie g(x) = int(x).
Je ziet hier de grafieken van beide. Hoe zit het met de differentieerbaarheid?

Antwoord

De grafiek van de functie f(x) = |x| bestaat uit twee halve lijnen die in (0, 0) bij elkaar komen. Daar zit een knikpunt. De functie is te schrijven als

$f(x)=\{\begin{array}{cc}x& \text{als }x\ge 0\\ -x& \text{als }x<0\end{array}$
De afgeleide is daarom $f\text{'}(x)=\{\begin{array}{cc}1& \text{als }x\ge 0\\ -1& \text{als }x<0\end{array}$

Je ziet dat het hellingsgetal links van 0 anders is dan rechts van 0.
De functie is voor x = 0 niet differentieerbaar.

De functie g(x) = int(x) rondt steeds een getal naar beneden af. De grafiek vertoont daarom sprongen zodra een x-waarde een geheel getal is.
In die waarden van x is de functie niet differentieerbaar.