Voorbeeld

Gegeven is de functie f(x) = x².
Stel een voorschrift op voor de afgeleide van deze functie.
Stel met behulp daarvan een vergelijking op van de raaklijn aan de grafiek van f voor x = 3.

Antwoord

Het differentiaalquotiënt voor willekeurige x is gelijk aan

$\underset{h\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{h\to 0}{\lim }\frac{{(x+h)}^2-x^2}{h}=\underset{h\to 0}{\lim }\frac{2xh+h^2}{h}=\underset{h\to 0}{\lim }\left(2x+h\right)=2x$

Dus de afgeleide is f'(x) = 2x.

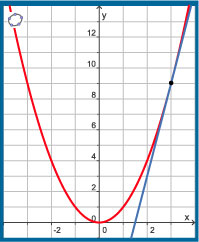
Wil je nu de vergelijking opstellen van de raaklijn aan de grafiek van f voor x = 3, dan heb je het hellingsgetal nodig voor die waarde van x. De afgeleide is het hellingsgetal van de grafiek van f voor willekeurige x, dus ook voor x = 3: f'(3) = 2 · 3 = 6.

Deze raaklijn heeft daarom een vergelijking van de vorm: y = 6x + b.
Omdat f(3) = 3² = 9, gaat deze raaklijn door het punt (3, 9).
Dit betekent dat: 9 = 6 · 3 + b en dus geldt: b = –9.

De vergelijking van de gevraagde raaklijn is y = 6x – 9.