Theorie

Bij exponentiële groei moet je per tijdseenheid steeds met hetzelfde getal vermenigvuldigen. Dit getal heet de groeifactor die bij die tijdseenheid hoort. Als g de groeifactor is dan geldt: g > 0.
Om vast te stellen of de groei exponentieel is, deel je opeenvolgende waarden van de hoeveelheid op elkaar. Komt daar steeds hetzelfde getal uit, dan is er sprake van exponentiële groei. De hoeveelheid op t = 0 noem je de beginwaarde.
Als een hoeveelheid met steeds hetzelfde percentage groeit is er sprake van exponentiële groei. Bij een groei met p procent hoort de groeifactor: g = 1 + $\frac{p}{100}$.
Voor p > 0 neemt de hoeveelheid toe en is g > 1.
Je spreekt dan van exponentiële toename.
Voor p < 0 neemt de hoeveelheid af en is g < 1 (maar groter dan 0).
Je spreekt dan van exponentiële afname.

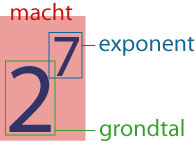
Bij exponentiële groei werk je met machten: vermenigvuldig je n keer hetzelfde getal g, dan schrijf je dat als gⁿ. Dit is een macht, de groeifactor g heet het grondtal, n heet de exponent, waarbij n (voorlopig) een positief geheel getal is.
Voor n = 0 is de afspraak: g⁰ = 1.

In het algemeen gelden voor een willekeurig grondtal g en willekeurige positieve gehele n en m de volgende rekenregels:
gⁿ · g^m = g^n + m           $\frac{g^n}{g^m}=g^{n-m}$           (gⁿ)^m = g^n · m