Theorie

Bij een formule zoals y = –x³ + 4x vind je bij elke waarde van x precies één waarde van y. In dat geval is y een functie van x met functievoorschrift y(x) = –x³ + 4x.

Bij een functie kun je een tabel maken en een grafiek tekenen. De invoerwaarden komen op de horizontale as, de x-as.
De uitkomsten heten functiewaarden.
y(1) = –1³ + 4 · 1 = 3 is de functiewaarde bij x = 1. Functiewaarden komen op de y-as.

Voor y(x) wordt ook wel f(x) gebruikt. y is dan een functie van x die f heet.
In praktijksituaties gebruik je vaak letters die verwijzen naar de betekenis van de variabelen. Bijvoorbeeld t voor tijd, l voor lengte, I voor inhoud, v voor snelheid, P voor vermogen, enzovoort. Je grafische rekenmachine werkt standaard met X voor invoerwaarden en Y voor functiewaarden.

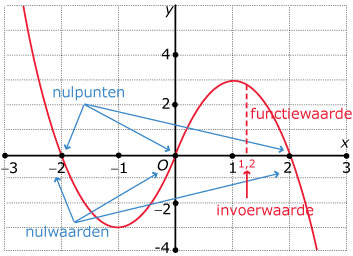
De nulwaarden van een functie zijn de invoerwaarden waarbij de functiewaarde (de uitkomst dus) 0 is. Bij de gegeven functie zijn het de x-waarden waarvoor geldt:
y(x) = –x³ + 4x = 0.
Hier zijn het de waarden x = 0, x = –2 en x = 2.
De bijbehorende nulpunten zijn (0, 0), (–2, 0) en (2, 0).