Theorie

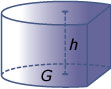
Je weet dat de inhoud (het volume) van alle figuren die de vorm hebben van een prisma of een cilinder met G als oppervlakte van het grondvlak en h als hoogte gelijk is aan G · h.
De inhoud I van een balk is daarom I(balk) = G · h = l · b · h.
De inhoud I van een rechte cilinder is daarom I(cilinder) = πr²h.

Je weet dat de inhoud (het volume) van alle figuren die de vorm hebben van een piramide of een kegel met G als oppervlakte van het grondvlak en h als hoogte gelijk is aan $\frac{1}{3}$ · G · h.
De inhoud I van een rechte kegel is daarom I(kegel) = $\frac{1}{3}$πr²h.
Volgens het principe van Cavalieri geldt dit alles ook voor scheve prisma's, piramides, cilinders of kegels, zolang h maar loodrecht op grondvlak (en bovenvlak) staat.

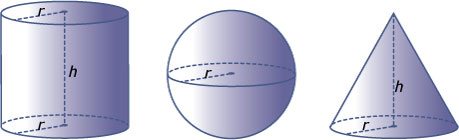
De de inhoud I van een bol is: I(bol) = $\frac{4}{3}$πr³.