Uitleg

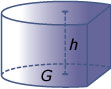
Je weet dat de inhoud (het volume) van alle figuren die de vorm hebben van een prisma of een cilinder met G als oppervlakte van het grondvlak en h als hoogte gelijk is aan G · h. Volgens het principe van Cavalieri geldt dit zelfs als het een scheef prisma of een scheve cilinder betreft, zolang h maar loodrecht op grondvlak (en bovenvlak) wordt gemeten.
De inhoud I van een rechte cilinder is daarom I(cilinder) = πr²h.

De beroemde Griekse wiskundige Archimedes (287 - 212 v.Chr.) hield zich veel bezig met het berekenen van de inhoud van lichamen. Hij ontdekte dat de inhouden van een (rechte) cilinder, een halve bol en een (rechte) kegel met dezelfde straal en hoogte zich verhouden als 3 : 2 : 1.
De inhoud van deze cilinder is πr² · r = πr³.
De inhoud van de halve bol is daar 2/3 deel en de inhoud van de kegel is daar 1/3 deel van.
Hiermee vind je voor de inhoud van een hele bol: I(bol) = 2 · $\frac{2}{3}$πr³ = $\frac{4}{3}$πr³.