Uitleg

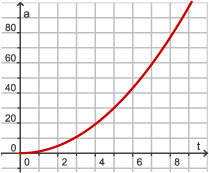
Hier zie je een afstandsgrafiek van een versnellende zeilwagen. Voor de afgelegde afstand a (in m) geldt a = 1,2t² waarin t de tijd in seconden is. De gemiddelde snelheid in m/s gerekend over de eerste 4 seconden is het differentiequotiënt:

$\frac{\Delta a}{\Delta t}=\frac{\mathrm{1,2}\cdot 4^2-\mathrm{1,2}\cdot 0}{4-0}=\frac{\mathrm{19,2}}{4}=\mathrm{4,8}$

Omdat de zeilwagen aan het versnellen is, zal de snelheid op t = 4 hoger zijn dan de gemiddelde snelheid over de eerste 4 seconden. Die snelheid op t = 4 kun je benaderen. Daarbij bereken je differentiequotiënten op steeds kleinere intervallen met 4 als beginwaarde.

Neem het interval [4;4 + h].
Het differentiequotiënt op dat interval is:

$\frac{\Delta a}{\Delta t}=\frac{\mathrm{1,2}\cdot {(4+h)}^2-\mathrm{1,2}\cdot 4}{4+h-4}=\frac{\mathrm{9,6}h+\mathrm{1,2}{h}^2}{h}=\mathrm{9,6}+\mathrm{1,2}h$   zolang h ≠ 0.

Dat is de gemiddelde snelheid in m/s op het interval [4,4 + h].
Laat je nu h naar 0 naderen, dan benadert 9,6 + 1,2h de grenswaarde 9,6.
Deze grenswaarde is de snelheid op t = 4. Je noteert dit als a'(4) = 9,6.
a'(4) is het differentiaalquotiënt voor t = 4, de (veranderings)snelheid op t = 4. In plaats van differentiaalquotiënt zeg je ook wel afgeleide waarde.