Soorten getallen

Inmiddels heb je ook leren worteltrekken. En dat levert twee problemen op...

Getallen als $\sqrt{2}$ kun je niet als breuk schrijven, het zijn irrationale getallen.
(Al in de Griekse Oudheid is dit bewezen.)
Daarom kun je dergelijke wortels alleen benaderen, nooit exact berekenen.
π is ook een voorbeeld van zo'n irrationaal getal.
Je moet dus aan de rationale getallen nog deze irrationale getallen toevoegen. Je krijgt dan de reële getallen. Dit zijn de getallen waar je eigenlijk altijd mee werkt. Alle reële getallen samen stel je voor door $ℝ$.

Het tweede probleem betreft getallen als $\sqrt{-1}$. Dit zijn geen reële getallen. Hiervoor zijn de complexe getallen in het leven geroepen, maar voorlopig krijg je daar niet mee te maken...

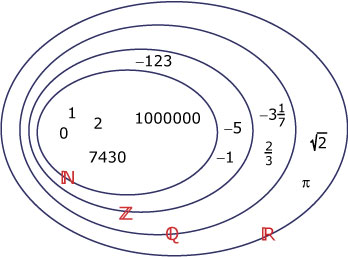
Hier zie je de voor jou belangrijke soorten getallen in één figuur.