Transformaties en differentiëren

Inleiding

Je hebt gezien, hoe handig differentiëren is bij het berekenen van hellingsgetallen. Alleen kun je dit nog maar op een beperkt aantal functies toepassen. Eigenlijk alleen op functies die bestaan uit machtsfuncties die je bij elkaar optelt (of van elkaar aftrekt).

Je gaat de techniek van het differentiëren uitbreiden naar transformaties van functies.

Je leert nu:

het differentiëren van functies van de vorm `f(x) + c`, `f(x + c)`, `c * f(x)` en `f(cx)`;
functiewaarden benaderen met behulp van differentiëren.

Je kunt al:

op een gegeven functie de vier basistransformaties toepassen, het bijpassende functievoorschrift opschrijven en de bijpassende grafiek tekenen;
aan een gegeven functie herkennen uit welke functie hij door transformatie kan ontstaan en welke transformaties dit dan zijn;
functies differentiëren met de machtsregel, de constanteregel en de somregel.

Verkennen

Maak op je grafische rekenmachine de grafiek van `f(x) = x^2` samen met zijn hellingsgrafiek `f'(x)`. Gebruik de standaardinstellingen van het venster.

> Maak de grafieken van `g_1(x) = (x - 4)^2`, `g_2(x) = x^2 - 3`, `g_3(x) = 1,5 * x^2`, `g_4(x) = (3x)^2` en `g_5(x) = 1,5(x - 4)^2 - 3`. Leg uit hoe steeds de afgeleide van `g` ontstaat uit die van `f`.

Uitleg

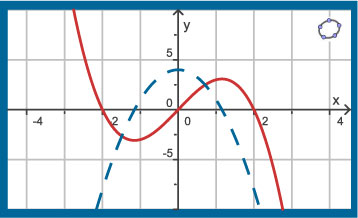
Hier zie je de grafiek van de functie `f(x) = -x^3 + 4x` (rood) samen met zijn afgeleide `f'(x) = -3x^2 + 4` (blauw gestippeld).

Je kunt nu zelf onderzoeken wat er met de afgeleide gebeurt als je op de gegeven functie een verschuiving of een vermenigvuldiging toepast. Ga met je grafische rekenmachine na dat:

Als de grafiek van `f` met `2` eenheden in de `y`-richting (dus omhoog) wordt verschoven ontstaat de grafiek van `f_1(x) = f(x) + 2` die precies dezelfde vorm heeft als de grafiek van `f` . (Hij ligt alleen hoger.) De hellingsgetallen veranderen door die verschuiving niet: de afgeleide van `f_1` is hetzelfde als die van `f`.
Kortweg: als `f_1(x) = f(x) + 2` dan is `f_1'(x) = f'(x)`.
Als de grafiek van `f` met `2` eenheden in de negatieve `x`-richting (dus naar links) wordt verschoven ontstaat de grafiek van `f_2(x) = f(x + 2)`. Op zich veranderen ook nu de hellingsgetallen niet, maar ze horen nu wel bij `x`-waarden die structureel `2` kleiner zijn.
Kortweg: als `f_2(x) = f(x + 2)` dan is `f_2'(x) = f'(x + 2)`.
Als je de grafiek van `f` met `2` vermenigvuldigt, worden alle functiewaarden `2` keer zo groot en krijg je `f_3(x) = 2 * f(x)`. Nu worden ook alle hellingsgetallen `2` keer zo groot.
Kortweg: als `f_3(x) = 2 * f(x)` dan is `f_3'(x) = 2 * f'(x)`.
Als je de grafiek van `f` met `2` vermenigvuldigt in de `x`-richting, krijg je de grafiek van `f_4(x) = f(2x)`. Nu worden de hellingwaarden niet alleen `2` keer zo groot, maar komen ze ook te voorschijn bij `x`-waarden die de helft kleiner zijn. Kortweg: als `f_4(x) = f(2x)` dan is `f_4'(x) = 2 * f'(2x)`.

Je gebruikt de afgeleide van een functie om de hellingwaarde in een punt van de bijbehorende grafiek te berekenen.
Daarmee kun je de functiewaarden in de directe omgeving van dat punt schatten. Je benadert dan de grafiek van de functie door zijn raaklijn. Als je maar genoeg inzoomt op de grafiek lijkt dat ook geen slechte benadering.

Omdat `f'(x) ~~ (f(x + h) - f(x))/h` geldt ook:

`f(x + h) ~~ f(x) + h * f'(x)`

Dit betekent dat `f(x + h)` kan worden benaderd vanuit `f(x)` met behulp van `f'(x)`. Natuurlijk alleen voor hele kleine waarden van `h`.

Bij de functie `f(x) = -x^3 + 4x` kun je dus `f(1,001)` benaderen vanuit `f(1) = 3` met behulp van `f'(1) = 1`.

Je vindt: `f(1,001) ~~ f(1) + 0,001 * f'(1) = 3 + 0,001 * 1 = 3,001`.

Vergelijk dit maar eens met de werkelijke functiewaarde `f(1,001) ~~ 3,000996999`.

‡

Opgaven

Voer de in de Uitleg beschreven transformaties op de grafiek van `f(x) = -x^3 + 4x` en zijn afgeleide uit. Ga na, dat je de resultaten vindt die daar zijn aangegeven.

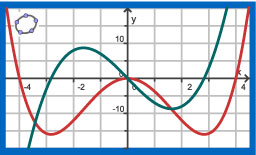In de figuur hiernaast zie je de grafiek van de functie `f(x) = 0,25x^4 - 4x^2` samen met zijn hellingsgrafiek, de grafiek van zijn afgeleide.
1. Maak de grafieken van `f` en `g_1(x)=f(x)+2` met de grafische rekenmachine. De afgeleide van `g_1 `is
  1. `g_1'(x) = f'(x)`
  2. `g_1'(x) = f'(x)+2`
2. Maak de grafieken van `f` en `g_2(x)=2*f(x)` met de grafische rekenmachine. De afgeleide van `g_2` is
  1. `g_2'(x) = f'(x)`
  2. `g_2'(x) = 2*(f'(x))`
3. Maak de grafieken van `f` en `g_3(x)=f(x+2)` met de grafische rekenmachine. De afgeleide van `g_3` is
  1. `g_3'(x) = f'(x)`
  2. `g_3'(x) = f'(x+2)`
4. Maak de grafieken van `f` en `g_4(x)=f(2*x)` met de grafische rekenmachine. De afgeleide van `g_4` is
  1. `g_4'(x) = f'(2*x)`
  2. `g_4'(x) = 2*(f'(2*x))`
5. Experimenteer met andere functies, en andere verschuivingen en vermenigvuldigingen. Ga na of je de differentieerregels voor transformaties van functies zoals die in de theorie staan zelf kunt vinden.

Theorie

Stel je de grafiek van een functie `f` voor met zijn afgeleide `f'`. (Zie: Uitleg.)

Pas je op de grafiek een verschuiving van `c` eenheden in de `y`-richting dan krijg je de grafiek van `f(x) + c` met als afgeleide `f'(x)`.
Dus de afgeleide van `f(x) + c` is `f'(x)`.

Pas je op de grafiek een verschuiving van `-c` eenheden in de `x`-richting dan krijg je de grafiek van `f(x + c)` met als afgeleide `f'(x + c)`.
Dus de afgeleide van `f(x + c)` is `f'(x + c)`.

Pas je op de grafiek een vermenigvuldiging met `c` in de `y`-richting dan krijg je de grafiek van `c * f(x)` met als afgeleide `c * f'(x)`.
Dus de afgeleide van `c * f(x)` is `c * f'(x)`.

Pas je op de grafiek een vermenigvuldiging met `1/c` in de `x`-richting dan krijg je de grafiek van `f(c * x) met als afgeleide `c * f'(c * x)`.
Dus de afgeleide van `f(c * x)` is `c * f'(c * x)`.

» Bewijs

Je kunt de afgeleide van een functie gebruiken om functiewaarden te benaderen.
Een lineaire benadering van `f(x + h)` is `f(x + h) ~~ f(x) + h * f'(x)`.

‡

Voorbeeld 1

De afgeleide van `f(x) = x^4` is `f'(x) = 4x^3`.
De afgeleiden van functies die door transformatie uit `f` ontstaan zijn te herleiden uit de afgeleide van `f`.

Als `f_1(x) = 2x^4` dan is `f_1'(x) = 2 * 4x^3 = 8x^3`.
Als `f_2(x) = x^4 + 2` dan is `f_2'(x) = 4x^3`.
Als `f_3(x) = (x + 2)^4` dan is `f_3'(x) = 4(x + 2)^3`.
Als `f_4(x) = (2x)^4` dan is `f_4'(x) = 2 * 4(2x)^3 = 8 * (2x)^3 = 64x^3`.

‡

Voorbeeld 2

De functie `H(t) = 2^t` heeft voor `t = 1` een hellingwaarde van `H'(1) ~~ 1,39`.

Welke hellingwaarde heeft de functie `K(t) = -3 * 2^(0,5t) + 10` voor `t = 2`?

Antwoord

Merk eerst op dat `K(t) = -3 * H(0,5t) + 10`.
Dus is de grafiek van `K` te maken door transformaties op de grafiek van `H` toe te passen: eerst vermenigvuldigen in de `t`-richting met `2`, dan vermenigvuldigen in de `H`-richting met`-3` en tenslotte `10` verschuiven in de `H`-richting.

Voor de afgeleide geldt daarom: `K'(t) = -3 * 0,5 * H'(0,5t)`.
Dus: `K'(2) = -3 * 0,5 * H'(1) ~~ -3 * 0,5 * 1,39 ~~ -2,085`.

Merk ook op dat je in dit geval niet `K'(1)` kunt afleiden uit `H'(1)`.

‡

Voorbeeld 3

Van een bewegend voorwerp is de afgelegde weg gegeven door een functie met voorschrift `s(t)` waarin `t` de tijd in seconden en `s` de afgelegde weg in meters is.

Na 5 seconden is de afgelegde weg 12 meter en de snelheid van het voorwerp 3 m/s.
Schat de afgelegde weg na 5,01 seconden.

Antwoord

Je kunt nu werken met een lineaire benadering van de gevraagde functiewaarde `s(5,01)`. Immers, de snelheid is de verandering van de afgeleide weg, dus de snelheid op een bepaald tijdstip is gelijk aan de afgeleide op dat tijdstip: `v(5) = s'(5)`.

De lineaire benadering gaat dan zo:
`s(5,01) ~~ s(5) + 0,01 * s'(5) = s(5) + 0,01 * v(5) = 12 + 0,01 * 3 ~~ 12,03` m.

‡

Opgaven

De afgeleide van `f(x) = x^4` is `f'(x) = 4x^3`. Van alle functies die door transformatie uit `f` kunnen ontstaan, kun je hiermee de afgeleide bepalen. Zie Voorbeeld 1.
1. Bepaal de afgeleide van `g(x) = (2x)^4`
2. Bepaal de afgeleide van `h(x) = 3(2x)^4+1`
3. Bepaal de afgeleide van `k(x) = 5 + 2(6 - 2x)^4`

Gegeven is de functie `f(x) = 5(x - 1)^3 + 4.`
1. De grafiek van `f` is door transformatie te herleiden uit die van `g(x) = x^3`. Welke transformaties moet je dan toepassen?
  1. Verschuiven in de positieve `x`-richting met 1 eenheid, dan verschuiven met 4 eenheden in de `y`-richting en tenslotte vermenigvuldigen in de `y`-richting met factor 5.
  2. Verschuiven in de negatieve `x`-richting met 1 eenheid, dan vermenigvuldigen in de `y`-richting met factor 5 en tenslotte verschuiven met 4 eenheden in de `y`-richting.
  3. Verschuiven in de positieve `x`-richting met 1 eenheid, dan vermenigvuldigen in de `y`-richting met factor 5 en tenslotte verschuiven met 4 eenheden in de `y`-richting.
2. Je weet dat `g(1)=3`. Bereken `f'(2)`. (Zie eventueel Voorbeeld 2.)

De grafiek van de functie `f(x) = 8^x` kun je maken door de grafiek van `g(x) = 2^x` te vermenigvuldigen in de `x`-richting.
1. Laat zien, dat `f(x) = g(3x)`.
2. De vergelijking van de raaklijn aan de grafiek van `g` voor `x=0` is bij benadering `y = 0,69x + 1`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=0`.

Gegeven is de functie `f(x) = x^3 - 4x`.
1. Bereken de richtingscoëfficiënt van de raaklijn aan de grafiek van `f` voor `x=1`.
2. Met behulp van dit hellingsgetal kun je de functiewaarden in de buurt van `x=1` schatten. Ze zijn ongeveer gelijk aan de `y`-waarden van de raaklijn aan de grafiek. Bekijk eventueel Voorbeeld 3. Benader `f(1,003)`.
3. Benader op dezelfde wijze `f(0,98)`.

Verwerken

De volgende functies kunnen ontstaan door transformatie van een bijpassende basisfunctie. Bedenk telkens welke basisfunctie dat is en bepaal dan de juiste afgeleide.
1. `y = 5x^4`
2. `y = 6(2x + 3)^4`
3. `f(x) = (x + 2)^5 - 100`
4. `y(t) = (2t + 4)^3`
5. `h(t) = 1 - 2(6 - 3t)^4`
6. `s(t) = 12(t - 10) + 2(t - 10)^2`

Van een functie `f` is het voorschrift niet bekend. De grafiek van `f` gaat door het punt `(1,6)`. De raaklijn aan de grafiek van `f` in dit punt heeft de vergelijking `y = 4x + 2`. De grafiek van de functie `g(x) = 3f(x) + 2` gaat door het punt `(1,20)`.
Stel een vergelijking op van de raaklijn aan de grafiek van `g` in dit punt.

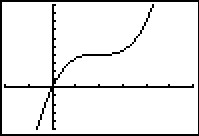Breng de grafiek van de functie `f(x) = 0,5(x - 2)^3 + 4` met je grafische rekenmachine zo in beeld als je hier ziet.
1. De grafiek heeft een symmetriepunt. Welk punt is dat?
2. Laat met behulp van de afgeleide zien waarom dit een symmetriepunt is.
3. Stel een vergelijking op van de raaklijn in het nulpunt van de grafiek van `f`.

De grafiek van de functie `f(x) = (1/2)^x + 4` kun je maken door de grafiek van `g(x) = 2^x` eerst te vermenigvuldigen in de `x`-richting en dan 4 eenheden te verschuiven in de positieve `y`-richting.
1. Met welke factor moet je de grafiek van `g` vermenigvuldigen?
2. De vergelijking van de raaklijn aan de grafiek van `g` voor `x = 1` is ongeveer `y = 1,38x + 0,62`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = -1`.
3. Waarom kun je `f'(1)` niet vinden met behulp van `g'(1)`?

Gegeven is een functie `f(x)` met `f'(1) = 2,75`.
Bereken `g'(1)` als `g(x) = f(3x - 2)`.

Van een functie `f` is gegeven dat `f(10) = 350` en `f'(10) = -12`.
Bepaal een lineaire benadering van `f(10,3)`.

Testen

Differentieer de volgende functies
1. `f(x) = (3x + 6)^5 - 20`
2. `g(x) = 16 - 2(x - 1)^4`
3. `K(q) = 200 + (60 + 3q)^3`

Gegeven is de functie `f(x) = a(x - b)^5` met `a != 0` en `b != 0`.
1. Hoe kun je de grafiek van `f` door transformatie laten ontstaan uit die van `y=x^4`?
  1. Verschuiven in de `x`-richting met `b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `a`.
  2. Verschuiven in de `x`-richting met `-b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `a`.
  3. Verschuiven in de `x`-richting met `b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `1/a`.
  4. Verschuiven in de `x`-richting met `-b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `1/a`.
2. Druk `f'(2)` uit in `a` en `b`.

De grafiek van de functie `g(x) = (1/3)^x + 5` kan door transformatie ontstaan uit die van `f(x) = 3^x`.
1. Welke transformaties moet je dan toepassen?
  1. Eerst vermenigvuldigen met `1/3` in de `x`-richting en dan de grafiek `5` eenheden in de positieve `y`-richting verschuiven.
  2. Eerst vermenigvuldigen met `-1` in de `x`-richting en dan de grafiek `5` eenheden in de positieve `y`-richting verschuiven.
  3. Eerst vermenigvuldigen met `-1` in de `y`-richting en dan de grafiek `5` eenheden in de positieve `y`-richting verschuiven.
2. De raaklijn aan de grafiek van `f` voor `x = 0` heeft de vergelijking `y = 1,1x + 1`. Stel een vergelijking op van de raaklijn aan de grafiek van `g` voor dezelfde waarde van `x`.

De slingertijd van de slinger van een klok wordt gegeven door `T = 2pi * sqrt(l/g)` waarin `T` de slingertijd in seconden en `l` de lengte van de slinger in meter is. De constante `g` noem je de gravitatieconstante en is ongeveer `9,8` m/s².
1. Een bepaalde klok loopt goed als zijn slingertijd 1 seconde bedraagt. Hoe lang moet de slinger dan zijn?
2. Benader met je grafische rekenmachine `T'(l)` voor de bij a berekende lengte van de slinger.
3. De lengte van de slinger neemt door uitzetting met 1% toe. Schat met een lineaire benadering met hoeveel seconden de slingertijd toeneemt.