Modellen

Inleiding

Een model is een vereenvoudigde weergave van de werkelijkheid.
In de wetenschap wordt veel met modellen gewerkt omdat de werkelijkheid te complex is om zonder meer te beschrijven. Door niet belangrijke details weg te laten (verstandige aannames te doen) kan een model worden opgesteld dat met wiskundige middelen is te beschrijven en door te rekenen. Uit het doorrekenen van het model worden conclusies getrokken die dan weer kunnen worden vergeleken met de realiteit.

Je leert nu:

• werken met modellen waarin het differentiëren kan worden toegepast;
• optimaliseringsproblemen aanpakken.

Je kunt al:

• differentiëren met alle differentieerregels;
• werken met de afgeleide onder andere voor het berekenen van extremen.

Verkennen

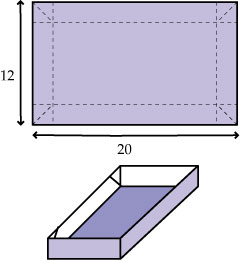
Een industrieel ontwerper ontwikkelt een type opbergbakje dat zuiver rechthoekige zijvlakken heeft. Het is van boven open en wordt gemaakt uit dunne rechthoekige plaatjes staal van 12 cm bij 20 cm die door een machine in de gewenste vorm worden gevouwen. De vierkantjes op de hoeken van een plaatje staal worden daarbij dubbel gevouwen en naar binnen geklapt. De bakjes krijgen een vlakke kunststof deksel die precies de bovenzijde afsluit.
De afmeting van de vierkantjes (de lengte van een zijde ervan) stel hij zo vast dat de inhoud van het bakjes zelf zo groot mogelijk wordt.

> Welke afmeting stelt hij in?

Uitleg

Bekijk het probleem bij "Verkennen" nog eens.
Vond je zelf de oplossing? Zo nee, lees dan verder...

Je maakt bij het probleem een geschikt wiskundig model. Je doet eerst een aantal aannames:

• het bakje met deksel is een zuivere balk zodat de inhoud eenvoudig is te berekenen;
• de vlakjes die naar binnen worden gebogen zijn zuivere vierkantjes met zijde x.

Vervolgens stel je voor de inhoud van het bakje een formule op.
Ga na, dat I = x(12 – 2x)(20 – 2x).
Aannames plus formule vormen je wiskundige model.
De maximale inhoud vind je met de GR of met behulp van differentiëren.
Ga na dat voor x ≈ 2,43 cm de inhoud maximaal is.

Opgaven

1. In de Uitleg zie je een globale uitwerking van het probleem van het opbergbakje met een zo groot mogelijke inhoud.
   1. Laat zien hoe je aan de formule voor de inhoud `I(x)` van het bakje komt.
   2. Bepaal nu de afgeleide van `I(x)` en bereken met behulp daarvan de waarde van `x` waarvoor `I` maximaal is.

Theorie

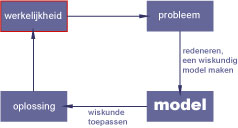
Wiskunde wordt veel toegepast in wetenschap en handel en industie om problemen op te lossen.
Daarmee wordt bedoeld dat bij een wetenschappelijk onderzoek, een nieuw te ontwikkelen technologie, een productieproces, en dergelijke vanuit de al bestaande praktijk een vraagstuk naar voren komt waar een antwoord op moet worden gevonden. Vaak heeft dat antwoord de vorm van een wiskundig model.
Een wiskundig model is een vereenvoudiging van de werkelijkheid op grond van verstandige aannames. In een goed model zijn alle belangrijke factoren nog aanwezig, alleen de onbelangrijke blijven buiten beschouwing. Meestal heeft het model de vorm van één of meer formules die beschrijven hoe de belangrijke variabelen zich gedragen.
Op die formules wordt dan de geschikte wiskundige theorie losgelaten...

Meer hierover vind je bij de rubriek "Probleemaanpak" op deze website.

Bij optimaliseren gaat het om wiskundige modellen waarbij wordt gezocht naar een maximale of een minimale waarde. Vaak is dat het maximum of minimum van een functie. Je kunt dat vinden met behulp van differentiëren of met je grafische rekenmachine.

Voorbeeld 1: literblik

Een blikfabriek maakt onder andere cilindervormige blikken voor de conservenindustrie. Er is veel vraag naar blikken met een inhoud van 1 liter. Voor de fabrikant is het belangrijk dat daar zo min mogelijk blik voor nodig is, dan blijven zijn kosten laag.
Welke afmetingen zal hij zijn literblikken geven?

Antwoord

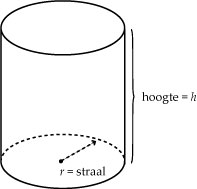
Neem aan dat elk blik zuiver cilindrisch is en dat de benodigde hoeveelheid blik gelijk is aan de totale oppervlakte van het blik. De twee bepalende variabelen zijn dan de straal van (het grondvlak van) het blik r en de hoogte h, neem beide in cm. Het gegeven betreft de inhoud van een blik (1 L = 1000 cm³), de eis betreft de oppervlakte die minimaal moet zijn.
Voor de inhoud van een cilinder geldt: I = πr²h.
Voor de oppervlakte van een cilinder geldt: A = 2πrh + 2πr².
Ga dat na.

Met I = 1000 vind je 1000 = πr²h en dus: $h=\frac{1000}{\pi r^2}$.
Als je nu in de formule voor A deze uitdrukking invult voor h, dan vind je: $A(r)=\frac{2000}{r}+2\pi r^2$.

Met behulp van differentiëren of de GR vind je nu dat voor x ≈ 5,4 cm en h ≈ 10,8 cm de totale oppervlakte minimaal is.

Voorbeeld 2: monopolist

ChemoTech brengt een nieuw onkruidbestrijdingsmiddel CHIF voor de landbouw op de markt. De productiekosten zijn hetzelfde als voor bestaande bestrijdingsmiddelen, er is een kostenmodel voorhanden: TK = 0,25q³ – 3q² + 18q + 30 waarin q het aantal kg (× 1000) CHIF voorstelt en TK de totale kosten in duizenden euro.
Voor de opbrengst wordt aangenomen dat 58500 kg/maand beschikbaar en dat bij een prijs van 18 euro per kg de verkoop 4500 kg/maand zal zijn. De verkoop q hangt lineair af van de prijs p. Welke winst kan ChemoTech met deze gegevens maximaal maken?

Antwoord

Uitgaande van ChemoTech als monopolist voor dit type onkruidbestrijdingsmiddel hangt de verkoop q lineair af van de prijs p. Het gaat daarbij dus op een functie van de vorm q = a · p + b waarvan de grafiek door (0; 58,5) en (18; 4,5) gaat.
Ga na dat daaruit volgt: q = –3p + 58,5.

Voor de totale winst TW geldt dan: TW = TO – TK als TO de totale opbrengst is. Omdat TK in q is uitgedrukt, wordt ook TW in q uitgedrukt:
TW = p · q – (0,25q³ – 3q² + 18q + 30) =
      = (19,5 – $\frac{1}{3}$q) · q – (0,25q³ – 3q² + 18q + 30).
Je ziet dat de formule voor q als functie van p hiervoor is herschreven.
De winstfunctie wordt dus: TW = –0,25q³ + 2$\frac{2}{3}$q² + 1,5q – 30.
De maximale winst is nu te vinden met behulp van differentiëren, de grafische rekenmachine of dit XL-model.

Voorbeeld 3: optimale bestelgrootte

Een winkelier die een bepaald product wil verkopen moet daarvan voldoende in voorraad hebben. Hij bestelt dit product bij de fabrikant. Daarvoor betaalt hij bestelkosten. Hoe vaker hij bestelt, hoe hoger de bestelkosten. Maar ja, als hij niet vaak bestelt moet hij zelf een grotere voorraad hebben en daarvoor maakt hij voorraadkosten.
Stel je voor dat de jaarlijkse vraag V exemplaren bedraagt, de bestelkosten B euro per bestelling zijn, elk exemplaar E euro kost en dat de voorraadkosten P procent van de kostprijs van de voorraad bedragen. De winkelier doet een aantal bestellingen per jaar van steeds evenveel exemplaren. Welke bestelgrootte is het gunstigst voor hem?

Antwoord

Noem de bestelgrootte x en ga er van uit dat hij jaarlijks V exemplaren koopt. Dan zijn:

• de kosten voor alle bestellingen samen B · $\frac{V}{x}$;
• de voorraadkosten te berekenen door uit te gaan van het in voorraad hebben van de halve bestelgrootte (aan het begin van de periode alle exemplaren, aan het einde niets meer, dus gemiddeld de helft), ze bedragen daarom $\frac{1}{2}$x · E · $\frac{P}{100}$.

De totale kosten voor de winkelier zijn dus: TK(x) = B · $\frac{V}{x}$ + $\frac{1}{2}$x · E · $\frac{P}{100}$ + V · E.
Van deze functie is met behulp van de afgeleide een minimum te berekenen.
De afgeleide is: $\frac{\text{d}TK}{\text{d}x}$ = $-B\cdot \frac{V}{x^2}+\frac{E\cdot P}{200}$ en $\frac{\text{d}TK}{\text{d}x}$ = 0 geeft: $x=\sqrt{\frac{200\cdot B\cdot V}{E\cdot P}}$.
Deze bestelgrootte levert de minste kosten voor de winkelier op.

Opgaven

2. Bekijk het probleem in Voorbeeld 1.
   1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
   2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan zelf de formule voor `A(r)` af te leiden.
   3. Bereken met behulp van differentiëren voor welke `r` de waarde van `A` minimaal is.


3. Bekijk het probleem in Voorbeeld 2.
   1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
   2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan de gegeven formule voor `TW` af te leiden.
   3. Bereken met behulp van differentiëren voor welke `q` de waarde van `TW` maximaal is.


4. Bekijk het probleem in Voorbeeld 3 .
   1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
   2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan de gegeven formule voor `TK` af te leiden.
   3. Laat met behulp van differentiëren zien een bestelgrootte van `x = sqrt((200 * B * V)/(E * P))` de minste kosten voor de winkelier oplevert.


5. Een bedrijf brengt droogtrommels op de markt. Er is een vraag naar droogtrommels van 1500 stuks per jaar. Voor de opslagkosten moet je rekenen met een rentepercentage van 9%. De productieprijs is € 700,=, en de prijs voor het plaatsen van een bestelling is € 25,=.
   1. Stel een formule op voor het verband tussen de totale bestelkosten en de bestelgrootte.
   2. Stel een formule op voor het verband tussen de opslagkosten en de bestelgrootte.
   3. Stel een formule op voor het verband tussen de totale kosten en de bestelgrootte.
   4. Bereken de optimale bestelgrootte.

Verwerken

6. Posters

   Op rechthoekige vellen papier van 1 m² worden foto’s afgedrukt om posters te maken. Om de foto blijft een rand wit: aan de onderkant een strook van 2 dm breedte, aan de andere drie randen stroken van 1 dm breedte.
   Bij welke afmetingen van de poster wordt de oppervlakte van het bedrukte deel zo groot mogelijk?
   1. Maak een schets van de situatie met de gegevens er in.
   2. Probeer eerst zelf het probleem op te lossen. Kijk pas als dat niet lukt naar c en d.
   3. Neem aan dat de breedte van zo’n poster wordt voorgesteld door `x` dm. Leid een formule af voor de oppervlakte `A` van het bedrukte deel als functie van `x`.
   4. Bereken met behulp van differentiëren de waarde van `x` waarvoor `A(x)` maximaal is.
   5. Beantwoord tenslotte de aan het begin gestelde vraag.



7. Ladderprobleem

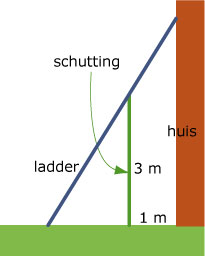   Iemand wil een ladder kopen om zijn dakgoten schoon te maken. Vlak naast zijn huis op 1 m van de muur staat echter een schutting van 3 m hoog. Hoe lang moet een ladder minstens zijn om over de schutting tegen de muur van het huis te komen?
   (Ga er van uit dat zowel de muur van het huis als de schutting loodrecht op de vlakke grond staan.)
   



8. Regenpakken

   Een kledingbedrijf introduceert een nieuw soort regenpak. Na verloop van tijd blijkt er een vraag te zijn van 1200 regenpakken per jaar. Voor de opslagkosten ga je uit van een rente van 7% per jaar. De productieprijs van een regenpak is € 35,=. De prijs voor het plaatsen van een bestelling is € 10,=.
   Bereken de optimale bestelgrootte.
   



9. Gas afbranden

   Een aantal jaren geleden werden voor het verbruik van aardgas twee tarieven gehanteerd:
   • Een tarief voor kleinverbruikers: iemand die jaarlijks tot 600 m3 aardgas verbruikte, betaalde 26 cent per m³ en een vastrecht van € 40,= per jaar.
   • Een tarief voor grootverbruikers: iemand die jaarlijks 600 m3 of meer verbruikte, betaalde 16 cent per m³ met een vastrecht van € 80,= per jaar.
   1. Teken de grafiek van de prijs `p` van het gasverbruik per jaar als functie van het aantal verbruikte m³ aardgas `a`.
   2. Geef zowel voor kleinverbruik als voor grootverbruik een passende formule.
   3. Voor welke waarde van a is er een "sprong" in de grafiek?
   Tuinders waarvan het gasverbruik in de buurt van de 600 m³ uitkwam lieten gas afbranden.
   4. Waarom en bij welke waarden voor `a` zouden ze dat hebben gedaan?
   5. Hoe moet het vastrecht voor grootverbruik worden aangepast om het afbranden van gas te voorkomen?
   6. Waarom blijft er dan nog altijd sprake van een "knik" in de grafiek?



10. Camping

    De eigenaar van een camping wil het aantal plaatsen uitbreiden. Hij koopt een hectare grond en wil daarop zuiver vierkante kampeerplaatsen inrichten. Hij heeft echter een deel van de grond nodig voor wegen, toilet- en wasgelegenheid, en dergelijke. Per kampeerplaats schat hij daarvoor zo’n 20 m2 te moeten reserveren. Verder gaat hij ervan uit dat het bedrag dat hij per plaats kan rekenen afhangt van de grootte ervan. In ieder geval rekent hij per nacht een prijs van € 4,50, maar daar bovenop denkt hij nog zo’n € 2,50 per meter breedte te kunnen vragen.
    Voor plaatsen van 4 m breedte zal hij dan € 14,50 per nacht kunnen rekenen, maar er kunnen er dan wel minder op zijn nieuwe terrein. De vraag voor deze campingeigenaar is daarom: "Hoe breed moet ik mijn kampeerplaatsen maken om zoveel mogelijk te verdienen aan deze extra hectare grond?"
    Los dat probleem voor hem op. Schrijf een volledige uitwerking op waarbij je van differentiëren gebruik maakt.
    

Testen

11. De prijs van yoghurt

    In een bepaalde supermarkt worden pakken yoghurt verkocht voor € 0,90 per stuk. Er worden elke week ongeveer 1000 pakken yoghurt verkocht. De bedrijfsleider denkt dat hij meer pakken yoghurt kan verkopen als hij de prijs verlaagt. Elke 4 cent prijsverlaging kon wel eens een omzetverhoging van 100 pakken betekenen. De pakken yoghurt worden ingekocht voor € 0,60 per stuk.
    1. Stel een formule op voor de winst als de functie van de verkoopprijs. Ga er daarbij van uit dat de bedrijfsleider gelijk heeft.
    2. Bij welke prijs is zijn winst maximaal? Hoe groot is de wekelijkse omzet dan?
    3. Is het verstandig om de prijs te verlagen?



12. Opslagruimte

    Een fabrikant heeft opslagruimte nodig. Het meest praktisch voor zijn producten is een rechthoekige loods met een vloeroppervlakte van 0,5 hm². Hij vraagt bij de gemeente de aankoop van een rechthoekig stuk grond op het industrieterrein aan om die loods op te kunnen bouwen. De gemeente antwoordt dat hem alleen een bouwvergunning kan worden verstrekt als hij een groenvoorziening om zijn loods aanbrengt. De voorschriften zijn: groenstroken aan de zijkanten en de achterkant van de loods van 5 m breed en een groenstrook aan de voorkant van 8 m breed. De fabrikant slaat nu aan het rekenen. Hij wil dit probleem oplossen: "Hoe kan ik een zo klein mogelijk rechthoekig stuk grond kopen waar een loods van 0,5 hm² op past en dat voldoet aan de voorschriften van de gemeente?"
    Los het probleem van de fabrikant op met behulp van differentiëren.