De quotiëntregel

Inleiding

Als je twee functievoorschriften f(x) en g(x) deelt, krijg je een nieuwe functie die de quotiëntfunctie van f en g heet. Soms kun je die quotiënten uitwerken, maar meestal niet.
Daarom moet je een differentieerregel hebben voor quotiëntfuncties f(x) / g(x).

Je leert nu:

• de regel voor het differentiëren van quotiëntfuncties;
• de quotiëntregel toepassen.

Je kunt al:

• allerlei soorten functies gebruiken;
• differentiëren met de machtsregel, de constante-regel, de somregel, de kettingregel en de productregel;
• werken met de afgeleide en de tweede afgeleide, onder andere voor het berekenen van extremen en buigpunten.

Verkennen

Een gebroken functie (quotiëntfunctie) heeft de vorm $f(x)=\frac{t(x)}{n(x)}$.

> Laat met een voorbeeld zien dat in het algemeen niet geldt: $f\text{'}(x)=\frac{t\text{'}(x)}{n\text{'}(x)}$.
> Hoe bepaal je de afgeleide van $f(x)=\frac{1}{x}$?
> Je kunt de functie $f(x)=\frac{t(x)}{n(x)}$ schrijven als $f(x)=t(x)\cdot {\left(n(x)\right)}^{-1}$.
Bepaal nu met behulp van de productregel en de kettingregel de afgeleide van f.

Uitleg

Als een deling niet uitkomt blijft er een breuk over. Ook bij functies kan dit voorkomen:

• $f(x)=\frac{3x^5}{2x^2}$ is een deling van t(x) = 3x⁵ en n(x) = 2x². Deze deling is echter te vereenvoudigen (mits x ≠ 0) tot f(x) = 1,5x³.
• $g(x)=\frac{x^2}{x-1}$ is een deling van t(x) = x² en n(x) = x – 1 die niet te herschrijven is tot een vorm zonder gebroken functie.

Bij functie f is een gesprek over hellingen, extremen, en dergelijke eenvoudig te voeren: je kunt deze functie na vereenvoudigen gemakkelijk differentiëren.

Bij functie g ligt dat anders. Het vinden van de afgeleide is daar minder eenvoudig. Maar onmogelijk is het niet.

Je schrijft de functie als: $g(x)=x^2\cdot {(x-1)}^{-1}$

En: $g\text{'}(x)=2x\cdot {(x-1)}^{-1}+x^2\cdot -1{(x-1)}^{-2}=\frac{2x}{x-1}-\frac{x^2}{{(x-1)}^2}$

Je ziet dat ook een gebroken functie is te differentiëren. Je krijgt alleen wel een vorm met twee breuken. Die kun je gelijknamig maken en optellen, maar het is handig om een regel af te leiden waarmee de afgeleide van een quotiëntfunctie ook weer als één quotiëntfunctie te voorschijn komt: de quotiëntregel voor differentiëren.

Opgaven

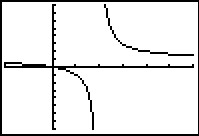1. Je ziet hier een deel van de grafiek van de functie `f(x) = x/(x - 2)`. Deze functie is een quotiëntfunctie.
   1. Wat is de teller en wat de noemer van deze functie?
   2. In de Uitleg kun je zien hoe je deze functie kunt differentiëren met de productregel en de kettingregel. Je moet daartoe de functie eerst herschrijven. Doe dat en bepaal de afgeleide.

Theorie

Voor de afgeleide van een quotiënt van twee functies geldt

Differentieerregel 7 (quotiëntregel):
Als $Q(x)=\frac{f(x)}{g(x)}$ (met g(x) ≠ 0) dan is $Q\text{'}(x)=\frac{f\text{'}(x)\cdot g(x)-f(x)\cdot g\text{'}(x)}{{\left(g(x)\right)}^2}$.

» Bewijs

De functie f is de teller van de breuk, de functie g is de noemer van de breuk.

Deze differentieerregel is niet altijd nodig, soms kun je een deling vereenvoudigen.
Vaak komt hij in combinatie met de voorgaande differentieerregels voor.
Vooral de kettingregel duikt daarbij vaak op!

Voorbeeld 1

In de Uitleg is de functie $g(x)=\frac{x^2}{x-1}$ gedifferentieerd met de productregel.
Doe dit nu met de quotiëntregel.

Antwoord

Bekijk eerst de teller en de noemer afzonderlijk:

• t(x) = x² met t'(x) = 2x
• n(x) = x – 1 met n'(x) = 1

Dus: $g\text{'}(x)=\frac{2x\cdot (x-1)-x^2\cdot 1}{{(x-1)}^2}=\frac{x^2-2x}{{(x-1)}^2}$

Ga na, dat deze afgeleide hetzelfde is dan de afgeleide die in de uitleg werd gevonden.

Voorbeeld 2

Differentieer de functie $f(x)=\frac{5x-10}{\sqrt{4+x^2}}$.

Antwoord

Met de quotiëntregel:

• t(x) = 5x – 10 met t'(x) = 5
• $n(x)=\sqrt{4+x^2}={\left(4+x^2\right)}^{\frac{1}{2}}$ met $n\text{'}(x)=\frac{1}{2}{\left(4+x^2\right)}^{-\frac{1}{2}}\cdot 2x=\frac{x}{\sqrt{4+x^2}}$

Dus: $f\text{'}(x)=\frac{5\cdot \sqrt{4+x^2}-(5x-10)\cdot \frac{x}{\sqrt{4+x^2}}}{{\left(\sqrt{4+x^2}\right)}^2}$

Vermenigvuldig nu teller en noemer met $\sqrt{4+x^2}$ en je vindt:

$f\text{'}(x)=\frac{5\cdot \left(4+x^2\right)-(5x-10)\cdot x}{\left(4+x^2\right)\sqrt{4+x^2}}=\frac{20+10x}{\left(4+x^2\right)\sqrt{4+x^2}}$

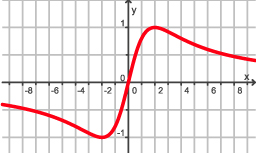
Voorbeeld 3

Hier zie je een deel van de grafiek van $f(x)=\frac{4x}{x^2+4}$.
Er zijn twee extremen. Bereken die met behulp van de afgeleide van f.

Antwoord

De afgeleide is: $f\text{'}(x)=\frac{4\cdot \left(x^2+4\right)-4x\cdot 2x}{{\left(x^2+4\right)}^2}=\frac{-4x^2+16}{{\left(x^2+4\right)}^2}$

Nu moet je de vergelijking f(x) = 0 oplossen. Met zo’n afgeleide ziet dat er misschien nogal dreigend uit, maar het valt reuze mee. Want: een breuk kan alleen maar op 0 uitkomen als de teller 0 is (en de noemer niet!).

Dit betekent dat –4x² + 16 = 0.
En deze vergelijking levert op: x = –2  V  x = 2.

De extremen zijn: max.f(2) = 1 en min.f(–2) = –1

Opgaven

2. Bekijk de grafiek van de functie `f(x) = x/(x - 2)` uit de vorige opgave nog eens. Je hebt de afgeleide bepaald met behulp van de productregel en de kettingregel. In de Voorbeeld 1 zie je hoe je de quotiëntregel voor differentiëren kunt gebruiken om van dergelijke functies de afgeleide te bepalen.
   1. Bepaal de afgeleide van `f` met de quotiëntregel.
   2. De afgeleide bij opgave 1 en die bij deze opgave zouden natuurlijk hetzelfde moeten zijn. Ga na dat dit inderdaad zo is.


3. Gegeven is de functie `f` door `f(x) = (x + 1)/(x)`.
   1. Bepaal van deze functie de afgeleide met behulp van de quotiëntregel.
   2. Je kunt ook het functievoorschrift eerst herschrijven. Dan hoef je de quotiëntregel helemaal niet te gebruiken. Bepaal nu de afgeleide zonder de quotiëntregel toe te passen. Welke van beide methodes van differentiëren is hier het handigst?


4. Differentieer de volgende functies (met de quotiëntregel als dat nodig is, bekijk eventueel Voorbeeld 2. Probeer telkens de handigste manier van differentiëren te gebruiken.
   1. `f(x) = (3x^2 - 4)/(2x + 1)`
   2. `f(x) = 4/(x - 2)^2`
   3. `f(x) = (3x - 1)/(sqrt(4 + x^2))`
   4. `f(x) = (x^2 - 1)/(x + 1)`


5. Gegeven is de functie `f(x) = x^3/(1 + x^4)`.
   1. Bereken de extremen van `f` met behulp van differentiëren. Geef benaderingen in twee decimalen nauwkeurig.
   2. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=2`.

Verwerken

6. Differentieer de volgende functies.
   1. `f(x) = (x + 1)/(x^2 - 16x)`
   2. `y(x) = 1/(x^2 - 4x + 5)`
   3. `H(t) = sqrt(2t + 6)/(3t)`
   4. `GTK(q) = (2q^3 - 10q^2 + 60q + 120)/q`
   5. `f(x) = (2x)/(x^2 - 10)`
   6. `y(x) = (-4)/(1 - 3x^2)`
   7. `A(r) = (2r)/(sqrt(4r + 8))`
   8. `GO(p) = 200p + 400 + 2000/p`


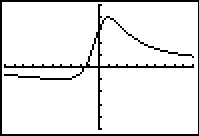7. Je ziet hier een deel van de grafiek van functie `f`. Het functievoorschrift is `f(x) = (8x + 12)/(x^2 + 4)`.
   1. Bereken algebraïsch de uiterste waarden van `f`.
   2. Los op: `f(x) < 3/2` .
   3. De grafiek van `f` snijdt de `x`-as in `A` en de `y`-as in `B`. Laat zien, dat de lijn `AB` de grafiek van `f` raakt.


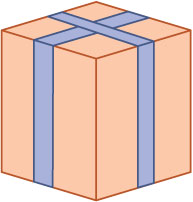8. De afdeling Verpakking van een bedrijf heeft de opdracht gekregen balkvormige doosjes te maken waarvan de lengte vier keer zo groot is als de breedte. Om elke doos worden twee zijden sierlinten aangebracht zoals je in de tekening ziet. De inhoud van de doosjes moet 1 liter zijn. Het bedrijf wil het verbruik van het sierlint zo klein mogelijk houden.
   1. Stel een formule op voor de lengte `L` van het benodigde sierlint als functie van de breedte `x` van de doos.
   2. Bereken met behulp van differentiëren bij welke afmetingen van het doosje de lengte van het sierlint zo klein mogelijk is. Geef je antwoord in millimeter nauwkeurig.


9. Voor de kosten van de productie van eenvoudige nietmachines heeft een bedrijf een wiskundig model laten opstellen. In dat model zijn de kosten `K` (in euro) afhankelijk van het aantal geproduceerde nietmachines `q` (in honderdtallen) volgens de formule `K = 4q^3 - 72q^2 + 600q + 2000`.
   De gemiddelde totale kosten zijn de kosten per nietmachine: `GTK = K/q`.
   1. Geef een functievoorschrift van `GTK(q)`.
   2. De verandering van de gemiddelde totale kosten afhankelijk van `q` wordt bepaald door de afgeleide `(text(d)GTK)/(text(d)q)`. Stel een formule op voor deze afgeleide.
   3. Er worden maandelijks maximaal 2000 van deze nietmachines geproduceerd. Breng de grafiek van `GTK` in beeld op je grafische rekenmachine. Bij welke vensterinstellingen komt het bijpassende deel van de grafiek geheel in beeld?
   4. Bij welke maandelijkse productie is `GTK` minimaal?


10. Een gelijkstroomcircuit bestaat uit een 12 volts batterij met een inwendige weerstand van 12 ohm en een variabele weerstand van `R` (ohm). Het vermogen `P` (in watt) dat door dit circuit wordt opgewekt, wordt gegeven door `P = RI^2`. De stroomsterkte `I` wordt daarin gegeven door `I = (12)/(R + 12)`.
    1. Druk het ontwikkelde vermogen uit in `R`, de variabele weerstand.
    2. Bereken het maximaal ontwikkelde vermogen met behulp van differentiëren.

Testen

11. Differentieer de volgende functies.
    1. `f(x) = (2x + 5)/(1 - x)`
    2. `g(x) = (sqrt(x))/(1 + x^3)`
    3. `H(t) = 1/(1 + 1/t)`
    4. `y(x) = (x^4 + 1)/(1 + x^2)^4`


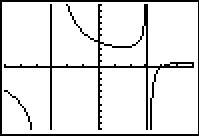12. Je ziet hier een deel van de grafiek van de functie `f(x) = (10x - 40)/(x^2 - 10)`.
    1. Bereken met behulp van de afgeleide de extremen van `f` in twee decimalen nauwkeurig.
    2. Het punt `(0,4)` ligt op de grafiek van `f`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in dat punt.


13. Een bedrijfseconoom heeft voor een fabriek van kleine gereedschappen een kostenanalyse gemaakt voor de productie van zogenaamde ‘allesknippers’. Hij geeft in zijn eindrapport een grafiek waarbij volgens hem de formule:

    `TK = 1/3 q^3 - 5q^2 + 40q`

    hoort. Hierin is `TK` in euro uitgedrukt en `q` de dagelijkse productie in tientallen.
    1. Stel een formule op voor de marginale kosten `MK = (text(d)TK)/(text(d)q)` als functie van q.
    2. Bereken `MK(1)`. Wat betekent dat getal? Hoe kun je het in de grafiek van `TK` vinden?
    3. Bij welke dagproductie is `MK` minimaal? Bepaal deze waarde zowel met je grafische rekenmachine als met algebraïsche methoden.
    4. Onder de gemiddelde totale kosten verstaan economen: `GTK = TK/q`. Bepaal met behulp van differentiëren voor welke waarde van `q` de gemiddelde totale kosten minimaal zijn.