Stochasten

Inleiding

Er bestaan variabelen waarvan de uitkomst afhangt van het toeval. Voorbeelden te over waarbij je wel telkens goed moet afspreken wat je onder dit toeval (en de grootte van de kansen) moet verstaan. Neem bijvoorbeeld het spel "darts". Voor iemand die zonder echt te mikken wel steeds zijn pijltje ergens op het dartbord weet te gooien zou je bij elke score kunnen spreken van toeval. Maar hoe stel je dit toeval vast? Kun je voor elke mogelijke score de kans erop vaststellen? En hoe dan wel?

Je leert nu:

het begrip (discrete) stochast (toevalsvariabele);
kansverdelingen opstellen;
werken met de verwachting en de standaardafwijking.

Je kunt al:

werken met frequentieverdelingen;
werken met gemiddelde en standaardafwijking bij frequentieverdelingen.

Verkennen

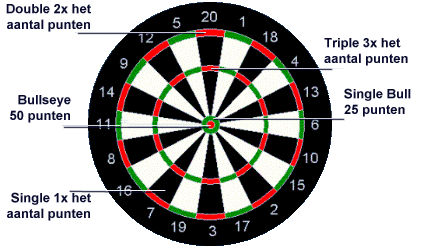
Hier zie je de indeling van een dartbord. De figuur is afkomstig van de website dartnet.nl en daar vind je ook een systeem van punten toekennen bij darts. Het aantal punten dat je bij een worp met één pijltje kunt scoren is vooral voor onervaren spelers van het toeval afhankelijk. Neem aan dat het aantal punten D als een toevalsvariabele kan worden opgevat.

> Verzin een manier om hiervoor een kansverdeling op te stellen.
> Is er verschil tussen ervaren of onervaren spelers v.w.b. de kansverdeling?
> Hoe bepaal je hoeveel punten je elke worp met een pijltje gemiddeld kunt verwachten?
> Hoe zou je een wereldranglijst van beste darters kunnen maken?

Uitleg

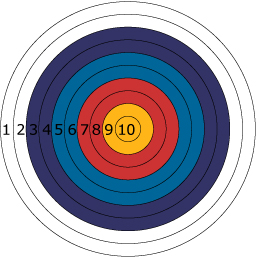
De kans dat je bij het handboogschieten de roos raakt is (tenzij je een prof bent) niet zo groot. In feite hangt die kans af van de schutter en kan hij alleen experimenteel worden bepaald. Alleen als je aanneemt dat iemand altijd het bord raakt en dat elke plek met even grote waarschijnlijkheid geraakt wordt, kun je proberen die kansen te beredeneren.
Maar hoe dan ook: het aantal punten dat je behaald met boogschieten met één pijl is een toevalsvariabele, een stochast. Omdat in dit geval het aantal mogelijke waarden dat de stochast kan aannemen eindig is, spreek je van een discrete stochast.
Bij een bepaalde schutter kun je de relatieve frequentie bepalen van elke mogelijke score. En dit kun je opvatten als kansverdeling van de stochast. Je stelt de stochast vaak voor met een hoofdletter, bijvoorbeeld X. Zo ziet een dergelijke kansverdeling er dan uit:

x	0	1	2	3	4	5	6	7	8	9	10
P(X = x)	0,02	0,02	0,04	0,10	0,09	0,11	0,12	0,12	0,15	0,15	0,08

Als je deze kansverdeling goed bekijkt zie je dat dit geen hele goede boogschutter is: de roos wordt maar in 8% van de gevallen geraakt en de spreiding is nogal groot. Hoeveel punten verwacht deze schutter per schot te halen?

Op grond van deze kansverdeling is de verwachting van het aantal punten per schot:
0 · 0,02 + 1 · 0,02 + 2 · 0,04 + 3 · 0,10 + 4 · 0,09 + 5 · 0,11 + 6 · 0,12 + 7 · 0,12 +
+ 8 · 0,15 + 9 · 0,15 + 10 · 0,08 = 6,22
De verwachtingswaarde is een maat voor de centrum van de verdeling.

Voor de spreiding gebruik je een maat die vergelijkbaar is met de standaardafwijking in de beschrijvende statistiek: je berekent eerst de verwachtingswaarde van de kwadraten van de verschillen van elke x-waarde met 6,22. Dat getal heet de variantie.
Vervolgens trek je uit die variantie dan weer de wortel. Dat geeft de standaardafwijking, een geschikte maat voor de spreiding van de kansverdeling.

‡

Opgaven

Bekijk de kansverdeling van de boogschutter de Uitleg.
1. Beschrijf hoe deze kansverdeling tot stand is gekomen.
2. Bereken zelf met de verwachtingswaarde. Beschrijf wat dit getal voor de boogschutter precies betekent.
3. Deze boogschutter schiet nu 15 keer op de roos. Hoeveel punten verwacht hij te behalen?

Bekijk in de Uitleg hoe je de standaardafwijking van de kansverdeling berekent.
1. Laat zien dat de standaardafwijking van de kansverdeling van de boogschutter ongeveer 2,56 is.
2. Teken een histogram van deze kansverdeling. Geef zowel de verwachtingswaarde als de standaardafwijking erin aan.
3. Waarom zal de kansverdeling van een redelijk goede boogschutter niet symmetrisch zijn?

"stochastikos" is Grieks voor "mikkend, gissend"

Theorie

Een toevalsvariabele is een variabele waar bij elke waarde een bepaalde kans hoort dat die waarde optreedt. In plaats van toevalsvariabele zeg je ook wel stochast. Als het aantal mogelijke waarden dat de stochast kan aannemen eindig is, spreek je van een discrete stochast.
Bij stochast X met waarden x₁, x₂, ..., x_n, hoort een kansverdeling, een tabel met kansen P(X = x_i) waarbij i = 1, 2, ..., n.

Zo'n kansverdeling kan worden beschreven door:

de verwachtingswaarde van de stochast, notatie E(X) of μ(X):

E(X) = x₁ · P(X = x₁) + x₂ · P(X = x₂) + ... x_n · P(X = x_n)
of korter: E(X) = $\sum_{i = 1}^{n} x_{i} \cdot P (X = x {}_{i})$ .

de standaardafwijking (of standaarddeviatie) van X, notatie σ(X):

de variantie van X is de verwachtingswaarde van de kwadraten van de verschillen x_i – E(X), en de standaardafwijking is de wortel uit de variantie, in formulevorm:
Var(X) = $\sum_{i = 1}^{n} {(x_{i} - E (X))}^{2} \cdot P (X = x {}_{i})$ en σ(X) = $\sqrt{Var (X)}$ .

‡

Voorbeeld 1

X is het aantal punten dat je bij boogschieten bij elk schot kunt behalen. Voor speler A zie je hier een kansverdeling voor X:

x	0	1	2	3	4	5	6	7	8	9	10
P(X = x)	0,02	0,02	0,04	0,10	0,09	0,11	0,12	0,12	0,15	0,15	0,08

Bereken bij deze kansverdeling de verwachting en de standaarddeviatie.

Antwoord

In de volgende figuur zie je de uitwerking.

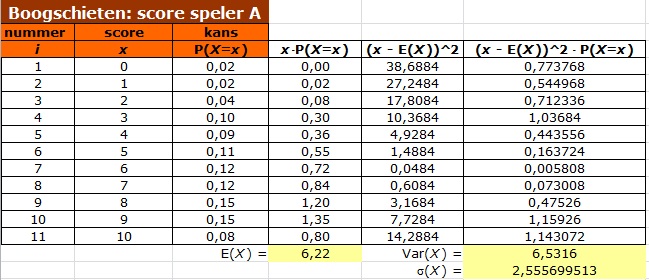
Je kunt Excel deze berekeningen ook rechtstreeks vanuit de kolommen x en P(X = x) laten doen. Hoe dit gaat vind je in de het practicum Statistiek met XL.

‡

Voorbeeld 2

Je kunt kansverdelingen en de bijbehorende verwachtingswaarde en standaardafwijking ook met de grafische rekenmachine bepalen.

Stochast X stelt het aantal ogen voor op het vlak dat boven komt na het werpen met een dobbelsteen. Stel een kansverdeling voor X op en bepaal de verwachting en de standaarddeviatie van X.

Antwoord

De kansverdeling van X noem je wel een uniforme kansverdeling want alle kansen zijn gelijk.

x	1	2	3	4	5	6
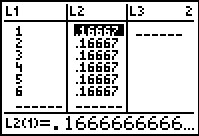
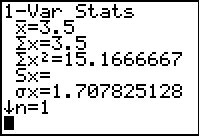P(X = x)	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$

Deze kansverdeling voer je in de grafische rekenmachine in, net als een frequentietabel.
De rekenmachine vindt nu E(X) = 3,5 want dit komt overeen met het gemiddelde van een frequentietabel. De bijbehorende standaardafwijking is σ(X) ≈ 1,71.
Ga dat na...

‡

Voorbeeld 3

Stochast X stelt het aantal ogen voor op het vlak dat boven komt na het werpen met twee dobbelstenen. Stel een kansverdeling voor X op en bepaal de verwachting en de standaarddeviatie van X.

Antwoord

De kansverdeling van X maak je vanuit het overzicht van alle 36 mogelijkheden.

x	2	3	4	5	6	7	8	9	10	11	12
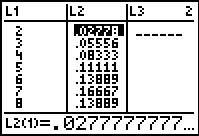
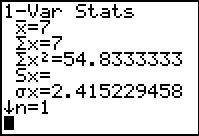
P(X = x)	$\frac{1}{36}$	$\frac{2}{36}$	$\frac{3}{36}$	$\frac{4}{36}$	$\frac{5}{36}$	$\frac{6}{36}$	$\frac{5}{36}$	$\frac{4}{36}$	$\frac{3}{36}$	$\frac{2}{36}$	$\frac{1}{36}$

Deze kansverdeling voer je in de grafische rekenmachine in, net als een frequentietabel.
De rekenmachine vindt nu E(X) = 7 en σ(X) ≈ 2,42.
Ga dat na...

‡

Opgaven

In Voorbeeld 1 zie je de berekening van de verwachtingswaarde en de standaardafwijking nog eens uitgewerkt.
Voor boogschutter B is stochast Y het aantal punten dat hij bij elk schot behaalt.

y 0 1 2 3 4 5 6 7 8 9 10

P(Y = y) 0,01 0,02 0,03 0,03 0,04 0,06 0,05 0,11 0,20 0,21 0,24
1. Bereken zijn verwachtingswaarde.
2. Bereken de standaarddeviatie van Y.
3. Vergelijk de twee frequentieverdelingen van de spelers A en B. Welke van beide is de betere schutter? En hoe zie je dat aan de verwachtingswaarden en de standaarddeviaties?

In Voorbeeld 2 zie je de kansverdeling bij het werpen met ��n dobbelstenen. Je ziet ook de berekening van de verwachtingswaarde en de standaardafwijking met behulp van het statistiekmenu van je grafische rekenmachine.
1. Voer zelf de kansverdeling in je grafische rekenmachine in.
2. Controleer de berekende verwachtingswaarde en standaarddeviatie.

Bij het werpen met twee dobbelstenen is de kans op het werpen van een 7 veel groter dan het werpen van een 12. In Voorbeeld 3 zie je een bijpassende kansverdeling.
1. Licht de kansen in deze kansverdeling toe.
2. Controleer de berekende verwachtingswaarde en standaarddeviatie.
3. Vergelijk het resultaat met dat uit de voorgaande opgave. Wat valt je op?

Bij het kansspel "Chuck-a-luck" wordt met drie dobbelstenen gegooid. Stel dat je speelt op het aantal vijven bij zo'n worp met drie dobbelstenen. Komt er ��n vijf voor, dan krijg je de inleg terug. Komen er twee vijven voor dan krijg je twee keer je inleg terug en komen er drie vijven voor dan krijg je maar liefst 10 keer je inleg terug.
Meteen meedoen dus...
1. Stochast A is het aantal vijven bij het werpen met drie dobbelstenen. Stel een bijbehorende kansverdeling op.
2. Een andere stochast is de uitbetaling U per ingelegde euro per worp. Stel ook een daarbij passende kansverdeling op.
3. Welke verwachtingswaarde en welke standaarddeviatie heeft U?
4. Ga je veel verdienen aan dit spel? Motiveer je antwoord.

Verwerken

Je staat met een sleutelbos met zes verschillende sleutels voor een gesloten deur en weet alleen maar dat precies ��n via sleutels gaat passen, niet welke dat is. Je probeert een sleutel. Als hij past, dan open je de deur. Past hij niet, dan houd je hem apart en probeer je een andere sleutel.
Noem het aantal sleutels dat je moet proberen totdat de deur open gaat `S`.
1. Bereken de kans dat de deur pas bij de zesde sleutel opengaat: P(S = 6).
2. Stel een kansverdeling op voor S.
3. Hoeveel sleutels verwacht je te moeten proberen?

Iemand heeft de tijd (in seconden) gemeten van een groot aantal proefpersonen, die ze nodig hadden om op een foto een bepaald voorwerp te herkennen. De resultaten staan in deze tabel.

t 1 2 3 4 5 6 7 8

P(T = t) 0,04 0,08 0,15 0,28 0,25 0,17 0,02 0,01

De relatieve frequenties kun je opvatten als de kansen dat het voorwerp na zoveel seconden werd gevonden.
1. Hoe groot is de kans dat het voorwerp door een willekeurige proefpersoon na 3 seconden wordt herkent? Hoe groot is de kans dat hij er langer over doet?
2. Hoeveel tijd verwacht je dat een proefpersoon nodig heeft om het voorwerp te herkennen? Welke standaardafwijking hoort daar bij?
3. Hoe groot is de kans dat de herkenningstijd die een proefpersoon nodig heeft meer dan een standaarddeviatie van de verwachtingswaarde afwijkt?

De eigenaar van een ijssalon verdient € 300,00 op een mooie dag. Bij minder goed weer heeft hij een verlies van € 60,00. De kans op een mooie dag is 0,3.
Hoeveel bedraagt de winstverwachting van deze kleine zelfstandige?

Wat is een redelijke inzet bij een spel waarbij je 1/5 kans hebt op een uitbetaling van € 25,00 en 2/5 kans op een uitbetaling van € 10,00?

Hoeveel meisjes mag je in een gezin met drie kinderen verwachten, als de kans op de geboorte van een meisje even groot is als die op de geboorte van een jongen?

Je wilt in een casino meedoen met het volgende spel: Na inzet van 1 euro mag je met drie dobbelstenen werpen. Gooi je ��n of meer zessen, dan krijg je je inzet terug plus voor iedere zes in de worp 1 euro extra.
1. Bereken de winstverwachting van dit spel.
2. Aan een andere tafel wordt hetzelfde spel gespeeld, maar nu met vier dobbelstenen. Ga door berekening na of hierdoor de winstverwachting verandert.

In een vaas zitten twee witte en drie rode balletjes. Uit deze vaas worden zonder teruglegging balletjes getrokken, net zolang tot er een wit balletjes wordt gettrokken.
Wat is de verwachting en de standaarddeviatie van het aantal benodigde trekkingen?

In een suikerfabriek staan twee machines voor het vullen van pakken suiker. Bij het afstellen op 1 kg blijken beide machines inderdaad pakken te vullen van ongeveer 1 kg, maar er komen toch wel behoorlijke afwijkingen voor. De volgende relatieve frequentieverdeling geeft dat weer:

x 970 980 990 1000 1010 1020 1030

Machine 1 P(X₁ = x) 0,04 0,07 0,12 0,18 0,25 0,29 0,05

Machine 2 P(X₂ = x) 0,00 0,00 0,15 0,30 0,35 0,20 0,00

Deze frequentieverdelingen kun je opvatten als kansverdelingen.
1. Toon aan dat beide kansverdelingen dezelfde verwachtingswaarde hebben. Hoe groot is die verwachting?
2. Teken bij beide kansverdelingen een kanshistogram op je grafische rekenmachine.
3. Welk bezwaar heb je wanneer als maat voor de spreiding het verschil tussen de grootste en kleinste waarde wordt genomen?
4. Bereken de variantie en de standaarddeviatie voor de stochasten X₁ en X₂ die behoren bij de beide vulmachines.
5. Hoeveel procent van de pakken suiker wijkt minder dan de standaarddeviatie van het gemiddelde af? Bereken dit percentage voor beide machines afzonderlijk.

Testen

Twee op papier even sterke tennissers hebben de finale bereikt van hun clubkampioenschap. Ze moeten onderling in een partij, waarbij het gaat om drie gewonnen sets, uitmaken wie zich clubkampioen van dat jaar mag noemen. Winnaar van de finale is dus diegene die het eerst 3 sets op zijn naam brengt.
Stochast T stelt het aantal te spelen sets voor.
1. Stel een kansverdeling voor T op.
2. Bereken E(T). Wat stelt dat getal in dit verband voor?

Je werpt vier keer met een zuivere dobbelsteen. Stochast X stelt het aantal zessen voor dat daarbij bovenkomt.
1. Stel de kansverdeling van X op.
2. Bereken de verwachtingswaarde en de standaardafwijking van X.

y	0	1	2	3	4	5	6	7	8	9	10
P(Y = y)	0,01	0,02	0,03	0,03	0,04	0,06	0,05	0,11	0,20	0,21	0,24

	x	970	980	990	1000	1010	1020	1030
Machine 1	P(X₁ = x)	0,04	0,07	0,12	0,18	0,25	0,29	0,05
Machine 2	P(X₂ = x)	0,00	0,00	0,15	0,30	0,35	0,20	0,00